Aufgabenstellungen


	SelMa-Team	Startseite	Lehrer Info	Aufgaben	teacher on demand
Aufgabenseite
Instruktionsphase	Selbstlernphase 1		Selbstlernphase 2	Präsentation	Abschluss
Aufgabe 1	Aufgabe 2	Aufgabe 6
	Aufgabe 3	(optional)
	Aufgabe 4	Aufgabe 7
	Aufgabe 5	(optional)

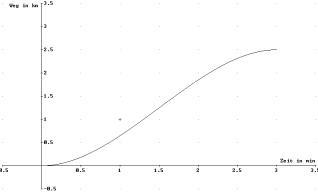
Aufgabe 1: Peter, der korrekte Autofahrer

Peter rühmt sich, ein besonders korrekter Autofahrer zu sein. "Gestern", so sagt er, "habe ich für die 2,5km lange Ortsdurchfahrt in Marl genau 180 Sekunden benötigt." War Peter so korrekt, oder hat er dabei nur Glück gehabt, dass an manchen Stellen keine Geschwindigkeitskontrolle war?
Die Auswertung des elektronischen Fahrtenbuchs, das die Fahrzeit und die zurückgelegte Strecke speichert, hat ergeben, dass die Weg-Zeit-Funktion ungefähr durch eine ganz-rationale Funktion dritten Grades beschrieben werden kann:
Fragen: a) Wie kommt Peter zu der Aussage, dass er ein korrekter Autofahrer ist? b) Wie müsste der Funktionsgraph aussehen, wenn Peter korrekt gefahren wäre? Geben Sie auch eine Funktionsgleichung an. c) In welchen Zeitabständen ist Peter schneller (langsamer) als 50 gefahren ? d) Peter hat erfahren, dass nach 1,5 Minuten Fahrzeit die Geschwindigkeit gemessen wurde. Muss er mit einem Bußgeldbescheid rechnen?

Aufgabe 2:

Galilei, Galileo (1564-1642), italienischer Physiker, Mathematiker, Philosoph und Astronom.

In der Physik entdeckte er die Fallgesetze und die Bewegungsgesetze von Geschossen. Sein Ansatz einer Mathematisierung der Naturwissenschaften übte einen großen Einfluss auf die neuzeitlichen Naturwissenschaften aus.

Galilei untersucht auch das Abrollen einer Kugel auf einer schiefen Ebene. Dabei maß er die Strecke s, welche die Kugel in der Zeit t zurücklegt. Er könnte folgende Tabelle zusammengestellt haben:

Zeit t (in Sekunden)	0	1	2	3	4	5	6	7	8	9	10
Strecke s (in Meter)	0	0,7	2,8	6,3	11,2	17,5	25,2	34,3	44,8	56,7	70

Wie konnte Galilei die Geschwindigkeit zur Zeit t ungefähr bestimmen ?

Unter der mittleren Geschwindigkeit (oder Durchschnittsgeschwindigkeit) im Zeitintervall versteht man das Verhältnis von Wegzuwachs zu Zeitzuwachs. Kurz:

Aufgabe 3:

Heute kann man mit Hilfe einer Digitaluhr und einer Lichtschranke die mittlere Geschwindigkeit in einem Zeitintervall leicht berechnen. Ein Versuchsfahrzeug gleitet jetzt auf einer schiefen Ebene hinunter. Die Lichtschranke wird an der Stelle s angebracht, an der die Geschwindigkeit gemessen werden soll. Oben auf dem Fahrzeug ist ein Stift der Breite Ds angebracht. Die Digitaluhr misst die Dunkelzeit Dt, die der Stift beim Passieren der Lichtschranke hervorruft.

Ist eine Zeitspanne gemessen, wird ein anderer Stift mit einer anderen Breite Ds angebracht und das Versuchsfahrzeug erneut gestartet. In der Tabelle sind die gestoppten Dunkelzeiten angegeben, die mit Stiften von 10 cm bis 2 cm Breite an der Stelle s = 0,5 m gemessen wurden.

Breite Ds (in Meter)	0,10	0,08	0,06	0,04	0,02
Zeit Dt (in Sekunden)	0,0427	0,0345	0,0261	0,0175	0,0088
mittlere Geschwindigkeit Ds/Dt

a) Berechnen Sie die mittleren Geschwindigkeiten und tragen sie diese in die Tabelle ein.

b) Stellen Sie die mittleren Geschwindigkeiten in Abhängigkeit von Dt graphisch dar und bestätigen Sie, dass die Werte um eine Gerade mit der Gleichung y = 2,02·Dt + 2,25 streuen.

c) Überlegen Sie, was diese Gerade mit der Momentangeschwindigkeit des Versuchfahrzeugs an der Stelle s = 0,5 m zu tun hat.

Aufgabe 4:

Mit einem Smart von 0 auf 100 in drei Sekunden! Die Mutprobe bei der RTL-100000 Mark Show am 1. April 2000
Car-Dropping der Superlative! An einem Spezialkran geht's mit dem Auto auf 60 m Höhe. Auf Franklins Kommando stürzen sie in die Tiefe - nur von einem Bungeeseil gehalten. Von 0 auf 100 in nur 3 Sekunden. Wird es ein Paar wagen? Wie würden Sie sich fühlen?
Überprüfen Sie, ob der PKW tatsächlich nach 3 Sekunden eine Geschwindigkeit von 100 km/h hat! In welcher Höhe zum Erdboden befindet sich der PKW in diesem Augenblick?
Hinweis aus der Physik: Die Bewegung eines Körpers im freien Fall kann durch die Weg-Zeit-Funktion s beschrieben werden. Mit t wird die Zeit in Sekunden bezeichnet und g die Fallbeschleunigung.	mit

Aufgabe 5:

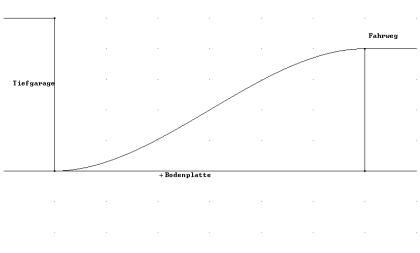
Tiefgarage

Bei dem Einfamilienhaus soll eine Zufahrt zu einer Tiefgarage angelegt werden. Der Fahrweg, der waagerecht verläuft, liegt 2m über der Bodenplatte. Tiefgarage und Fahrweg haben einen Abstand von 6m. Der Architekt schlägt vor, den Übergang zum Garagenboden und zum Fahrweg "möglichst glatt" (ohne Knick) anzulegen. Die Fahrbahn der Zufahrt soll durch eine ganz-rationale Funktion 3. Grades beschrieben werden.

Die Fahrbahn soll durch die Funktion f beschrieben werden. Der Ursprung des Koordinatensystems liegt am Übergang des Garagenbodens zur Auffahrt.

In der "Mitte der Auffahrt" hat der PKW die größte Steigung zu überwinden. Welche Steigfähigkeit muss der PKW haben, um diese Stelle überwinden zu können?

Steigfähigkeit: Angabe einer Steigung in Prozent, die von einem Fahrzeug kurzfristig überwunden werden kann.

Aufgabe 6: (optional)

Ein Alternativvorschlag für der Garagenzufahrt: Die Fahrbahn wird durch eine abschnittsweise definierte Funktion f beschrieben:

Ist diese Funktion für eine Fahrbahnkonstruktion geeignet?

Welche Steigfähigkeit muss der PKW im Punkte M(3/2) besitzen.

Aufgabe 7: (optional)

Meteorkrater Der abgebildete Meteorkrater ist ein erdgeschichtlich bedeutendes Monument. Er entstand vor ca. 30.000 Jahren, als ein Meteorit mit ca. 60.000 km/h auftraft. Der Meteorkrater dient heute - wegen seiner Beschaffenheit - der NASA als Trainingscamp für Astronauten oder als Kulisse für Film und Video-Shows.
Ein direkter Weg von der Kratersohle bis zum Rand des Kraters wird näherungsweise durch die Funktion f beschrieben. Ein Filmteam soll mit einem Geländewagen zu den täglichen Dreharbeiten transportiert werden. Der Hersteller eines Geländefahrzeugs behauptet, dass dieses Steigungen bis zu 100% bewältigen kann. Es soll nun ein Zufahrtweg angelegt werden.
Von welchem Punkt an sind Erdarbeiten erforderlich, so dass der oben beschriebene Geländewagen das Team in und aus dem Krater befördern kann? Machen Sie einen Vorschlag für die Profillinie der Trasse.

Lernen durch Lehren Arbeitsteilig werden in Gruppen die folgenden Themen erarbeitet, mit dem Ziel, dieses Wissen an die Mitschülerinnen und Mitschüler weiterzugeben.
Thema 1	Funktionenmikroskop
Thema 2	Lokale graphische Darstellung des Differenzenquotienten zu einer Stelle a: Lochpunktverfahren
Thema 3	Algebraische Vereinfachung von Differenzenquotienten: x-Methode
Thema 4	Algebraische Vereinfachung von Differenzenquotienten: h-Methode	Bilder zum Gruppenpuzzle

Präsentation phase
Partnergruppen stellen ihre Lösungen zu den Aufgaben 2 bis 7 vor.

Eine mögliche Definition des Ableitungsbegriffs Die Funktion f sei auf einem Intervall I definiert und . Wenn der Differenzenquotient für einen Grenzwert besitz, so heißt die Funktion f an der Stelle a differenzierbar. Man nennt den Grenzwert die Ableitung von f an der Stelle a und schreibt f ' (a) .
	Der Ableitungsbegriff ist ein zentraler Begriff in der Infinitesimalrechnung Sir Isaac Newton (1643-1727) und Gottfried Wilhelm Leibniz (1646-1716) entwickelten zwischen 1665 und 1677 unabhängig voneinander die Differential- und Integralrechnung. Mit der Meraner Konferenz (1905) kam die Infinitesimalrechnung in den Mathematikunterricht der Gymnasien.

Die Mutprobe bei der RTL-100000 Mark Show am 1. April 2000