Funktionenmikroskop

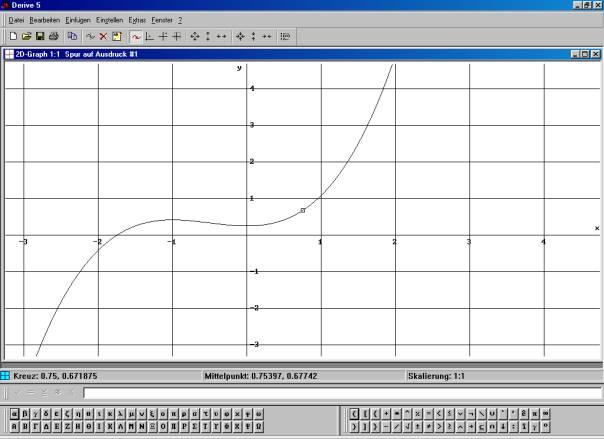
Betrachtet man den Graphen einer Funktion f in der Nähe eines festen Punktes P(a/f(a)) mit einem "Mikroskop" , so erkennt man, dass das beobachtete kleine Graphenstück bei hinreichend starker Vergrößerung praktisch geradlinig verläuft und somit eine gewisse Steigung besitzt.

Dieses ist die Steigung von f an der betreffenden Stelle a.

Beispiel:

Betrachtete Stelle: a = 0,75, der Kurvenpunkt hat die Koordinaten: P(0,75/0,671875)

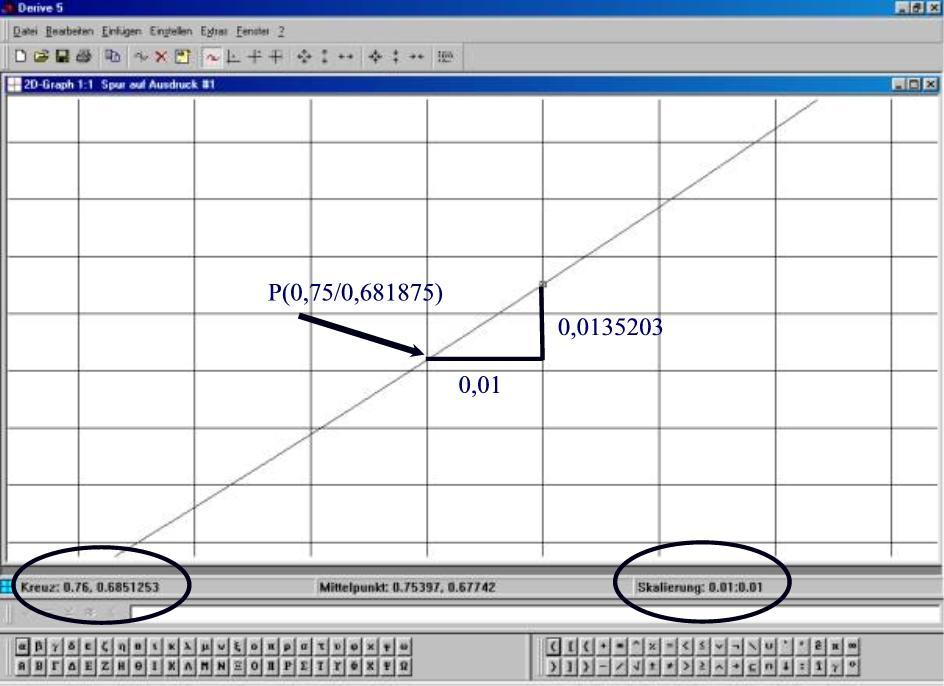
Durch mehrfaches Zoomen erreicht man, dass der Funktionsgraph in dem dargestellten Intervall "geradlinig" verläuft. Die Steigung dieser Geraden kann nun berechnet werden.

Mit Hilfe des Spurmodus kann man nun die Koordinaten von einem zweiten Punkt Q auf dem Graphen bestimmen: Q(0,76/0,6851253) . Aus den Koordinaten der beiden Punkte läßt sich nun die Steigung berechnen: m = 1,352503

Ein Funktionenmikroskop kann man mit dem Graphikmodus eines CAS leicht selbst erstellen.

Bauanleitung für ein Funktionenmikroskop mit oder mit dem