Bestimmung der Tangentensteigung mit der x-Methode
Gesucht ist die Tangentensteigung der Funktion f an der Stelle a = 0,75
|
|
 |
Berechnung von Steigungen von Sekanten durch Q(x / f(x)) und P(0,75 / f(0,75))
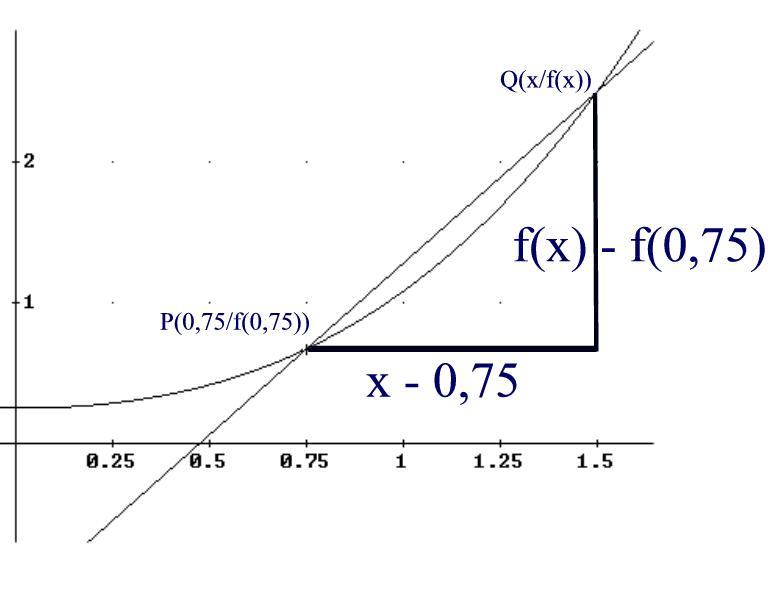
| Punkt Q | Steigung der Sekante | Sekantensteigung m |
| Q(0 / f(0)) | m = (f(0) - f(0,75)) : (0 - 0,75) | 0,5625 |
| Q(2 / f(2)) | m = (f(2) - f(0,75)) : (1 - 0,75) | 3,3958 |
| Q(x / f(x)) allgemein | m = (f(x) - f(0,75)) : (x - 0,75) |
Man erhält damit eine Funktion, die jeder Stelle x die Sekantensteigung durch Q(x / f(x)) und P(0,75 / f(0,75)) zuordnet. Man nennt diese Funktion Sekantensteigungsfunktion.
 bzw.
bzw. 
Berechnet man den Funktionswert vom m für einen x-Wert in der "Nähe von 0,75", so erhält man ein Ergebnis, das der gesuchten Tangentensteigung recht nahe kommt. Aber der interessante Wert für x=0,75 kann natürlich nicht berechnet werden, da der Nenner für diesen Wert 0 wird. Aber gleichzeitig wird auch für x=0,75 der Zähler gleich 0. Der Bruch muss genauer analysiert werden.
Vereinfacht man den Bruch mit Hilfe von einem CAS algebraisch, so erhält man eine neue Funktion, die in allen Werten mit m übereinstimmt. Außerdem ist die neue Funktion an der Stelle 0,75 definiert:

Für diese Funktion kann nun der Funktionswert an der Stelle x = 0,75 berechnet werden. Es gilt:

Dieser Wert ist nun die Steigung der Tangente an der Stelle x = 0,75.