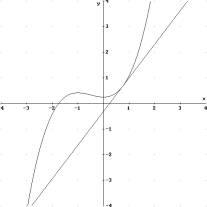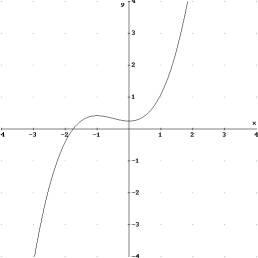
Bestimmung der Tangentensteigung mit der h-Methode

Gesucht ist die Tangentensteigung der Funktion f an der Stelle a = 0,75

Man betrachtet erst einmal Steigungen von Sekanten durch zwei Punkte auf dem Graphen: Q(x / f(x)) und P(0,75 / f(0,75))

Setzt man x - 0,75 = h, so ist x = 0,75 + h.

Man erhält die Sekantensteigungen nun durch Berechnung von Steigungen von Sekanten durch Q(0,75+h / f(0,75+h)) und P(0,75 / f(0,75))

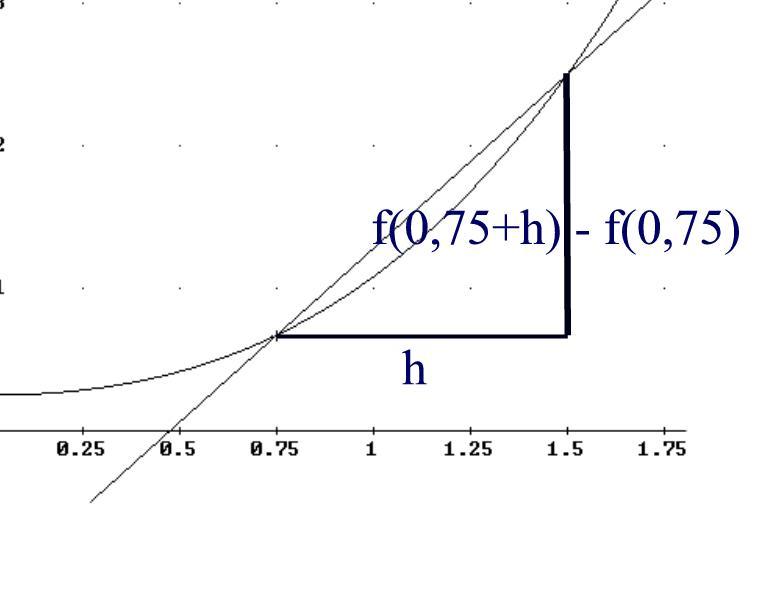
Man erhält damit eine Funktion, die für jedes h die Sekantensteigung durch Q(0,75+h / f(0,75+h)) und P(0,75 / f(0,75)) angibt:

bzw

.

Berechnet man den Funktionswert von m für h-Werte "in der Nähe von 0", so erhält man ein Ergebnis, das der Steigung der Tangente an der Stelle a = 0,75 recht nahe kommt. Aber der interessante Wert für h=0 kann natürlich nicht berechnet werden, da der Nenner für diesen Wert 0 wird. Aber auch der Zähler nimmt für h=0 den Wert 0 an. Der Bruch muss genauer analysiert werden.

Vereinfacht man den Bruch mit Hilfe von einem CAS algebraisch, so erhält man eine neue Funktion, die in allen Werten mit m übereinstimmt. Außerdem ist die neue Funktion für h=0 definiert:

Für diese Funktion kann nun der Funktionswert an der Stelle 0 berechnet werden. Es gilt:

Dieser Wert ist nun die Steigung der Tangente an der Stelle x = 0,75 .