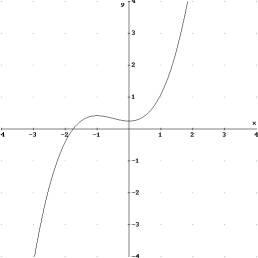
Gesucht ist die Tangentensteigung der Funktion f an der Stelle a = 0,75
|
|
 |
Berechnung von Steigungen von Sekanten durch Q(x / f(x)) und P(0,75 / f(0,75))
| Punkt Q | Steigung der Sekante | Sekantensteigung m |
| Q(0 / f(0)) | m = (f(0) - f(0,75)) : (0 - 0,75) | 0,5625 |
| Q(2 / f(2)) | m = (f(2) - f(0,75)) : (1 - 0,75) | 3,3958 |
| Q(x / f(x)) allgemein | m = (f(x) - f(0,75)) : (x - 0,75) |
Man erhält damit eine Funktion, die jeder Stelle x die Sekantensteigung durch Q(x / f(x)) und P(0,75 / f(0,75)) zuordnet. Man nennt diese Funktion Sekantensteigungsfunktion.
Allgemeine Sekantensteigungsfunktion von f zur Stelle a: ![]()
Mit Hilfe von CAS kann man den Graphen dieser Sekantensteigungsfunktion darstellen.
|
Graph der Sekantensteigungsfunktion von f zur Stelle a = 0,75 Für a = 0,75 ist die Funktion nicht definiert, an dieser Stelle hat der Graph eine Lücke.
|
|
|
|
Man kann nun das Kreuz in die Lücke plazieren. Der Punkt S(0,75 / 1,3125) schließt die Lücke im Graphen. 1,3125 wird der Lückenwert der Sekantensteigungsfunktion genannt. |
|
|
| Dieser Lückenwert liefert die exakte Tangentensteigung. |
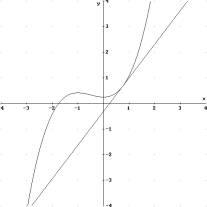 |
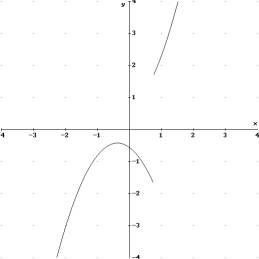
Nicht immer existiert ein Lochpunkt
|
Beispiel:
Stelle a = 0,75 |
|
|
|
Graph der Sekantensteigungsfunktion von f zur Stelle a = 0,75 Hier kann die Lücke nicht durch einen Punkt geschlossen werden. Es existiert keine Tangente. |
 |
Das allgemeine Verfahren:
Die Steigung der Tangente an den Graphen einer Funktion im Punkt P(a / f(a)) kann nach folgendem Verfahren gewonnen werden:
(1) Man bestimmt die Steigung der Sekante durch den Kurvenpunkt P und einen weiteren Kurvenpunkt Q(x / f(x)).
![]()
(2) Man untersucht die Sekantensteigungsfunktion und überprüft, ob der Graph an der Stelle a einen Lochpunkt aufweist.
(3) Die zweite Koordinate des Lochpunktes liefert die Steigung der Tangente.