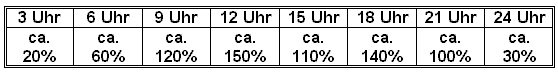Differentialrechnung - Bestimmung von Funktionsgleichungen

Baustein 2 - 7(11)

Aufgaben aus dem Bereich der Medizin

Aufgabe 2: Leistungs- oder Bereitschaftskurve

Die folgende Darstellung zeigt die durchschnittliche Arbeitsleistung eines Arbeitnehmers in Abhängigkeit von der Tageszeit bemessen auf seine Durchschnittsleistung ( = 100%). Ein Teilbereich der Leistungskurve soll durch den Graphen einer ganzrationalen Funktion angenähert werden.

(Quelle: http://gwv-fachverlage.de/wilex/daten/262.htm)

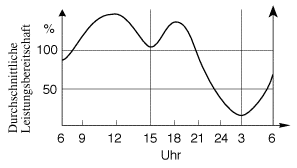
2.1 Beschreiben Sie mit eigenen Worten den Verlauf der Kurve!

Die exakte Bestimmung der Gesamtkurve erfordert das Lösen eines recht großen linearen Gleichungs-systems, was an dieser Stelle den Rahmen sprengen würde. Daher soll nur ein Teil der Leistungskurve
aus den vorgegebenen Bedingungen bestimmt werden und zwar die Kurve zwischen 15 Uhr und 24 Uhr.

In folgender Tabelle sind die ungefähren Leistungsprozentzahlen über den Tag verteilt angegeben:

2.2 Stellen Sie die für die Bestimmung von f (im Bereich 15 bis 24 Uhr) notwendigen Bedingungen auf !
      Bei 21 Uhr soll ein Wendepunkt liegen, aus dem Graphen lassen sich bei 15 Uhr und 18 Uhr weitere             Informationen gewinnen.
     
      Lassen Sie Prozent (%) beim Aufstellen der Bedingungen weg !
      Stellen Sie auch für die gefundenen Bedingungen das zugehörige lineare Gleichungssystem auf !

      Das Lösen des gefundenen Gleichungssystems mit DERIVE ist nun nicht verlangt, da die Eingabe
      der gewonnenen Gleichungen doch recht mühsam ist. Daher ist der Funktionsterm in der Lösung nur
      angegeben. Er wird noch bei Aufgabe 2.3 gebraucht!

2.3 Um wieviel Uhr (ungefähr!) zwischen 15 Uhr und 24 Uhr ist die Arbeitsleistung noch etwa 50%?
       Lösen Sie mit DERIVE !

      Minimieren Sie dazu den Internet Browser (oben rechts, linker Button) und rufen Sie das Programm       DERIVE auf ! Kehren Sie danach wieder in den Lehrgang zurück!