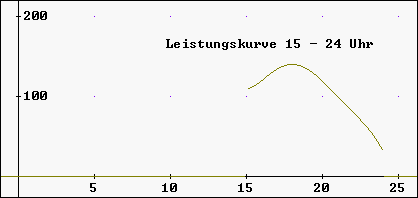
Leistungskurve: Lösung zu Aufgabe 2.2

Es ergibt sich folgendes Gleichungssystem:

(1) f(15) = 110 Û a·15⁶ + b·15⁵ + c·15⁴ + d·15³ + e·15² + g·15 + h = 110
(2) f '(15) = 0 Û 6·a·15⁵ + 5·b·15⁴ + 4·c·15³ + 3·d·15² + 2·e·15 + g = 0
(3) f(18) = 140 Û a·18⁶ + b·18⁵ + c·18⁴ + d·18³ + e·18² + g·18 + h = 140
(4) f '(18) = 0 Û 6·a·18⁵ + 5·b·18⁴ + 4·c·18³ + 3·d·18² + 2·e·18 + g = 0
(5) f ''(21) = 0 Û 30·a·21⁴ + 20·b·21³ + 12·c·21² + 6·d·21 + 2·e = 0
(6) f(21) = 100 Û a·21⁶ + b·21⁵ + c·21⁴ + d·21³ + e·21² + g·21 + h = 100
(7) f(24) = 30 Û a·24⁶ + b·24⁵ + c·24⁴ + d·24³ + e·24² + g·24 + h = 30

Zur Lösung dieses Gleichungssystems benutzt man entweder den Befehl
SOLVE([F(15) = 110, F'(15) = 0, F(18) = 140,...],[a,b,c,d,e,g,h])
oder man löst das Gleichungssystem mit dem Befehl SOLVE > SYSTEM.

DERIVE liefert als Funktionsterm (vergleichen Sie hierzu den DERIVE-File Leistung.mth):

Als Graph ergibt sich mit DERIVE unter Verwendung der CHI-Funktion (Eingabe:
CHI(15,x,24)*F(x) ):