"Der Graph zu f hat an der Stelle x₀ eine Wendestelle" bzw. "hat einen Wendepunkt
   bei W(x₀ / y₀)" bedeutet:

f ''(x₀) = 0 .

Bei dem zugehörigen Wendepunkt W(x₀ / y₀) ändert sich das Krümmungsverhalten des Graphen zu f (s. u.).

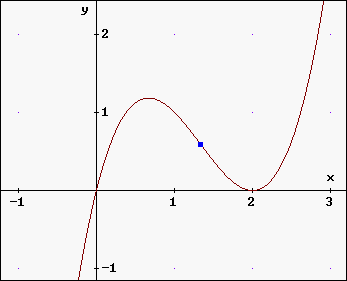
Beispiel: Die Polynomfunktion f mit der Gleichung f(x) = x³ - 4x² +4x hat bei x₀ = 4/₃ eine Wendestelle (also einen Wendepunkt W(4/₃ ; y_w) ; vgl. mit untenstehendem Graph):