Koordinatengeometrie - Lineare Funktionen und ihre Graphen

Baustein 2 - 5(7)

Kinderfest in der Biliothek: Abstand zwischen Punkt und Polygonzug

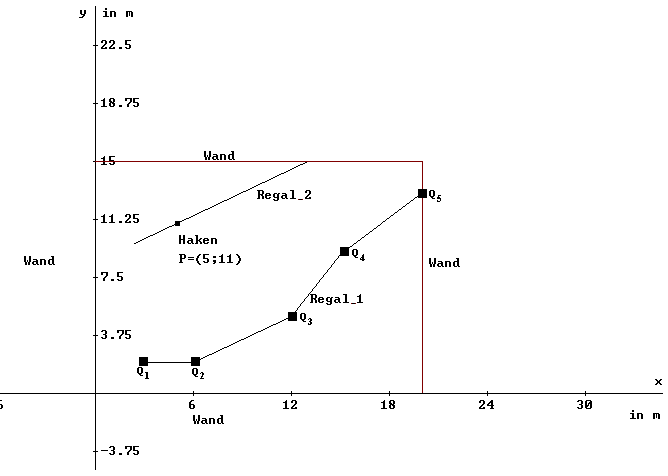
In der folgenden Aufgabe 11 soll nun schrittweise der kürzeste Abstand zwischen dem Haken und dem gegenüberliegenden Regal berechnet werden. Aus Aufgabe 10 ist bereits der kürzeste Abstand zwischen dem Haken und dem Regalstück zwischen Q₂ und Q₃ bekannt. Er beträgt etwa d=8,497. Hier zur Erinnerung noch einmal die Abbildung und die gegebenen Punkte.

Punkte auf dem Polygonzug (Eckpunkte des Regal_1 im Raum)

Aufgabe 11

Berechnen Sie den Abstand zwischen dem Punkt P und der Geraden durch Q₁ und Q₂.

Berechnen Sie den Abstand zwischen dem Punkt P und der Geraden durch Q₃ und Q₄.

Berechnen Sie den Abstand zwischen dem Punkt P und der Geraden durch Q₄ und Q₅.

Plotten Sie in DERIVE das Geradenstück zwischen den Punkten Q₄ und Q₅ (nicht die gesamte Gerade!) und den Schnittpunkt der beiden Geraden aus 11.3.
Zum Zeichnen des Geradenstücks ist die CHI-Funktion hilfreich.
Was beobachten Sie?

Berechnen Sie den Abstand zwischen P und Q₄ und den Abstand zwischen P und Q₅.
Zeichnen Sie von Hand die Punkte P, Q₄ und Q₅ in ein Koordinatensystem und entscheiden Sie aufgrund Ihrer Zeichnung, welcher Punkt auf dem Geradenstück zwischen Q₄ und Q₅ am nächsten zu P liegt!

Beanworten Sie die ursprüngliche Fragestellung: Wie lang muss die Schnur sein, die vom Haken P zum gegenüberliegenden Regal gespannt wird und wo muss sie befestigt werden?

Beschreiben Sie in Stichworten die Vorgehensweise bei der Berechnung des Abstands eines Punktes P zu einem Polygonzug (Streckenzug).