Koordinatengeometrie - Lineare Funktionen und ihre Graphen |
Lösung |
Lösung zu Aufgabe 11.2
Man berechnet nacheinander:
- Die Gerade durch Q3 ( 12 | 5 ) und Q4 ( 15 | 9 ) :
Die Steigung der Geraden durch Q3 und Q4 ist
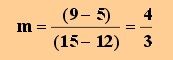
Durch Einsetzen in die Punkt-Steigungsform erhält man die Geradengleichung:
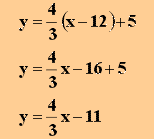
- Die Lotgerade zur Geraden durch Q3 und Q4, die
durch den Punkt P(5 | 11) verläuft:
Die Lotgerade hat die Steigung:
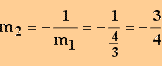
Durch Einsetzen in die Punkt-Steigungsform erhält man die Geradengleichung:
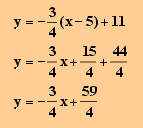
- Der Schnittpunkt S der beiden Geraden:
Man berechnet zunächst die x-Koordinate:
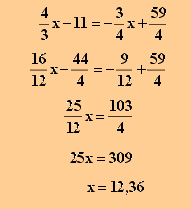
und anschließend die y-Koordinate:
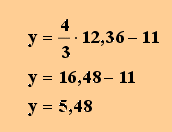
Der Schnittpunkt ist demnach S=(12,36 | 5,48)
- Den Abstand zwischen dem Schnittpunkt S und P:
Durch Einsetzen in die Abstandsformel erhält man:
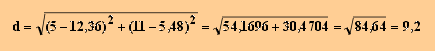
Die Berechnungen mit DERIVE finden Sie in der Datei Aufgabe 11-2.mth .
|
|
|