Übungsaufgaben zur Kontrolle des Lernerfolgs

Koordinatengeometrie - Lineare Funktionen und ihre Graphen

Baustein 1 - 13(13)

Übungsaufgaben zur Kontrolle des Lernerfolgs

Aufgabe 12
In Aufgabe 7 wurden folgende Geraden berechnet:

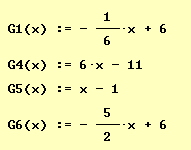12.1

Berechnen Sie mit DERIVE den Schnittpunkt von g₁ mit g₄ !
Wie weit (d = ? ) ist der Punkt P₃(2 | 1) von der Geraden g₁ entfernt?
Rechnen Sie auch hier mit DERIVE !

12.2

Die Geraden g₁, g₅, und g₆ schließen ein Dreieck ein (vergleichen Sie im Graphikfenster!).
Berechnen Sie von Hand unter Zuhilfenahme eines Taschenrechners den Umfang des Dreiecks!
Berechnen Sie dann von Hand unter Zuhilfenahme eines Taschenrechners das Flächenmaß für das Dreieck!
Zur Erinnerung:
[ g = Länge der Grundseite, h =Länge der Höhe auf die Grundseite]

12.3

Der Graph einer linearen Funktion g verläuft durch den Punkt P(-2 | -3) und schneidet die y-Achse bei x = 3. Wie lautet die zugehörige Funktionsgleichung?
Berechnen Sie außerdem von Hand unter Zuhilfenahme eines Taschenrechners den Abstand der Geraden vom Koordinaten-Ursprung.

12.4

Der Klavierlehrer Wolfgang Amadeus Taste muss umziehen. Er schaut sich verschiedene Wohnungen an. Eine Wohnung gefällt ihm besonders gut, aber ihm fällt auf, dass der Flur sehr verwinkelt ist. Er fragt sich, ob es wohl möglich ist, seinen Flügel (aufrecht, auf seinen Rollen) durch diesen Flur zu transportieren.
Er macht sich dazu folgende Skizze (Ansicht von oben):

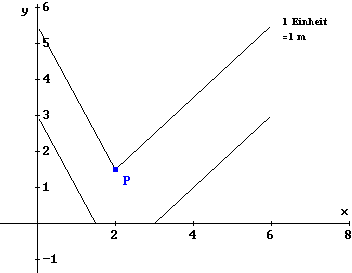
Die Geradenstücke, die die Wände (unten) darstellen, sind definiert durch:
f(x) := - 2 x + 3
g(x) := 0
h(x) := x - 3
im Bereich 0 £ x £ 1,5
im Bereich 1,5 £ x £ 3
im Bereich 3 £ x £ 6

Der Punkt P hat die Koordinaten ( 2 | 1,5 ).
Der Flügel ist 148 cm breit und 165 cm lang.

Wie breit ist die engste Stelle im Flur?
Passt der Flügel durch den Flur? Begründen Sie.