Differentialrechnung - Bestimmung von Funktionsgleichungen |
Baustein 5 - 2(3) |
|
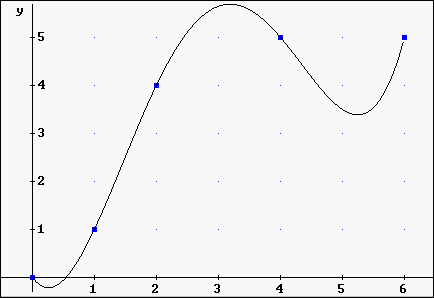
Approximation durch Spline-Interpolation - Fortsetzung Aufgabe 1 Die vorgegebenen 5 Punkte sind: P0(0/0), P1(1/1), P2(2/4), P3(4/5), P4(6/5) Betrachtet man das Ergebnis unserer ersten Näherung, so ist dieses mehr oder weniger enttäuschend. Auch sind beim Biegen eines Lineals nicht solch ausgeprägte Krümmungen bzw. Ausbuchtungen zu erwarten. Das geht sicherlich auch aus der von Ihnen gezeichneten Kurve für das gebogene Lineal hervor. Aus diesen Gründen ist dieser Ansatz mittels einer einzigen ganzrationalen Funktion für eine Approximation unzureichend. Man kann nun dennoch eine möglichst gute und glatte Näherungskurve (für das Lineal) durch einen anderen Ansatz gewinnen: Sind n+1 viele Punkte P0, P1, ... , Pn vorgegeben, so wählt man für jedes der n vielen Teilintervalle zwischen den Punkten eine andere ganzrationale Funktion, deren Graphen sich aber glatt aneinanderfügen. Dies erreicht man dadurch, dass an jeder Nahtstelle xs für je zwei Teilfunktionen f1 und f2 gilt: (1.) f1(xs) = f2(xs) und (2.) f1'(xs) = f2'(xs) und (3.) f1''(xs) = f2''(xs) In Worten: Bei xs müssen
die beiden Teilfunktionen f1 und f2 im Funktionswert Für die Randstellen x0 und xn setzt man üblicherweise die zweite Ableitung gleich Null. Sind alle Teilfunktionen vom Grad 3, so nennt man die Gesamtfunktion einen kubischen Spline . So erhält man zum Beispiel bei 4 vorgegebenen Punkten 3 Teilfunktionen mit je 4 zu bestimmenden Koeffizienten, also insgesamt 12 Koeffizienten. Bei unserem Lineal sind es 5 vorgegebene Punkte und daher 4 Teilfunktionen mit je 4 zu bestimmenden Koeffizienten.
|
|
|
|