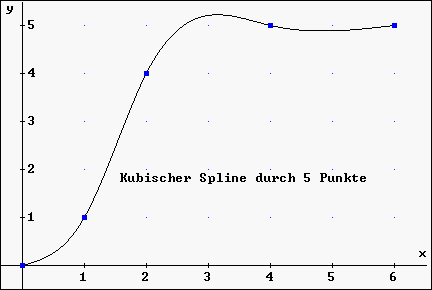
Approximation durch Spline-Interpolation: Lösung zu Aufgabe 1-2

Da 5 Punkte (sogenannte "Knoten" oder "Stützpunkte") vorgegeben sind, erhält man zunächst 4 Intervalle, für die die Teilfunktionen des kubischen Splines zu finden sind:

Diese Teilintervalle sind: [0; 1], [1; 2], [2; 4] und [4; 6].

Daher werden für den kubischen Spline 4 Spline-Funktionen (ganzrationale Funktionen 3. Grades) benötigt:

(Beachten Sie: z. B a2 entspricht dem Koeffizienten a₂ usw.)

Die sich aus den 4 Intervallen ergebenden "Stützstellen" x_s sind:
x_s=0 (Randstelle), x_s=1, x_s=2, x_s=4, x_s=6 (Randstelle).

Für die zu bestimmenden Spline-Funktionen ist gefordert:

1.) Übereinstimmung der Funktionswerte bei x_s (und Randstellen):
F1(0)=0, F1(1)=1, F2(1)=1, F2(2)=4, F3(2)=4, F3(4)=5, F4(4)=5, F4(6)=5

2.) Übereinstimmung der ersten Ableitungen bei x_s (ohne Randstellen):
F1'(1)=F2'(1), F2'(2)=F3'(2), F3'(4)=F4'(4)

3.) Übereinstimmung der zweiten Ableitungen bei x_s (und Randstellen):
F1''(0)=0, F1''(1)=F2''(1), F2''(2)=F3''(2), F3''(4)=F4''(4), F4''(6)=0

DERIVE liefert als Lösung dieses Gleichungssystems:
(Dazu verwendet man den Befehl SOLVE([F1(0)=0,F1(1)=1,...],[a1,b1,c1,d1,a2,...]) oder man löst das obige Gleichungssystem mit dem Befehl Solve > System.)

Die Berechnungen hierzu finden Sie im DERIVE-File  Approximation2.mth im Anhang!
Ausdruck des Graphen, der Ihrer Zeichnung wohl nahe kommen dürfte:

Zum Vergleich: Kubischer Spline und erste Approximation durch eine ganzrationale Funktion 4. Grades:

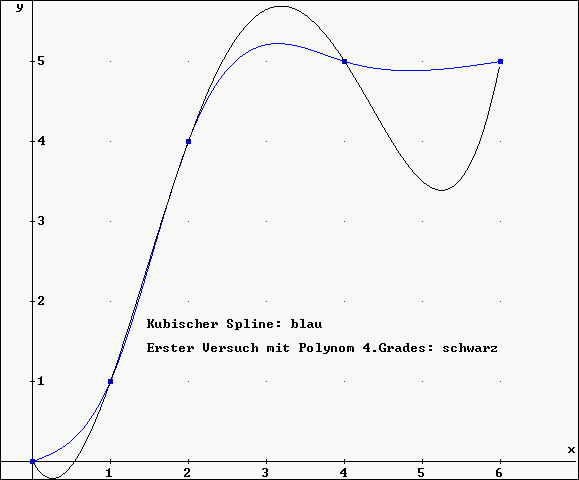
Eine kubische Spline-Interpolation durch möglichst viele einzelne Kurvenstücke von Polynomfunktionen 3. Grades ist einer Interpolation durch nur ein Gesamtpolynom hohen Grades klar überlegen ist. Man kann sagen:
Je höher die Anzahl der vorgegebenen Stützstellen (Knoten) ist, desto überlegener ist der kubische Spline einer Interpolation durch nur ein Gesamtpolynom, dessen Graph durch alle Knoten verläuft.

Und: Durch geeignete Verengung der Stützpunktabstände kann man starken Abweichungen (Überschwingern) vorbeugen.