|
Dieser Baustein ist nur für
Interessierte gedacht, also nicht klausurrelevant!
Wenn Sie unten auf der Seite auf den Doppelpfeil klicken, können Sie diesen
Baustein überspringen. Sie gelangen dann direkt zu einem
Programm, mit dem Sie Ihre Kenntnisse über den Zusammenhang von Funktionsgraphen
und Funktionsgleichungen testen und verbessern können.
Approximation (Annäherung)
durch Spline-Interpolation - Vorbemerkungen
Spline ist der englische Ausdruck für ein
biegsames Lineal, das früher verwendet wurde bei der Konstruktion
von Schiffskörpern: durch vorgegebene Punkte (sogenannte Knoten
oder Stützpunkte) wurde eine "glatte" Kurve gezeichnet.
Die Spline-Interpolation, die in diesem Baustein 5 vorgestellt
wird, findet Anwendung in der Mess- und Regeltechnik bei der Darstellung
von Sensorkennlinien, in der graphischen Datenverarbeitung, bei
der "glatten" Darstellung mathematischer Funktionsverläufe
und dient u. a. der Konturbeschreibung in der digitalen Bildbearbeitung.
Auch bei der Konstruktion von Automobil-Profilen spielt sie eine
Rolle.
Zunächst soll einmal ein biegsames
Lineal durch 5 vorgegebene Punkte gelegt werden, die in untenstehendem
Schaubild zu sehen sind:
(Die Idee und die numerischen Grundlagen zu dieser Problemstellung
entstammen dem Buch von Hans-Jürgen Kayser, Analysis mit DERIVE.
Dümmlers Verlag Bonn 1996, Seite 109 ff.)
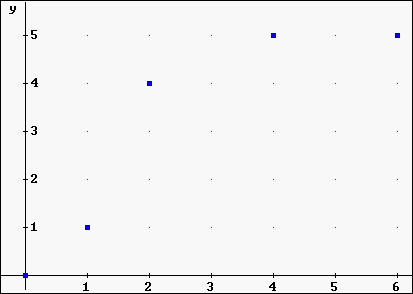
Die vorgegebenen 5 Punkte (Knoten) sind: P0(0/0),
P1(1/1), P2(2/4), P3(4/5), P4(6/5).
Durch diese Punkte soll der Graph (das Lineal) verlaufen.
|
Aufgabe 1:
Bevor Sie mit der Bearbeitung
der Aufgabe 1.1 beginnen, sollten Sie einmal auf einem Blatt
Papier die 5 Punkte in einem Koordinatensystem eintragen und
eine "glatte" und "schöne" Kurve
einzeichnen, die Ihrer Meinung nach das gebogene Lineal darstellt.
Vergleichen Sie dann später Ihre Zeichung mit den Ergebnissen
der Aufgaben 1.1 und 1.2 !
1.1 Bestimmen Sie (zuerst)
die Gleichung einer ganzrationale Funktion f kleinsten
Grades, deren Graph
durch die angegebenen
Punkte P0, P1, ... , P4 verläuft!
Stellen Sie
dazu die notwendigen Bedingungen auf und lösen Sie das
zugehörige lineare
Gleichungssystem mit DERIVE
!
Stellen Sie auch den
Graphen zu f im Graphikfenster von DERIVE dar!
Minimieren Sie dazu den Internet
Browser (oben rechts, linker Button) und rufen Sie das Programm
DERIVE auf ! Kehren
Sie danach wieder in den Lehrgang zurück!
|
|
|