Differentialrechnung - Bestimmung von Funktionsgleichungen

Baustein 2 - 5(11)

Aufgaben aus dem Bereich der Biologie

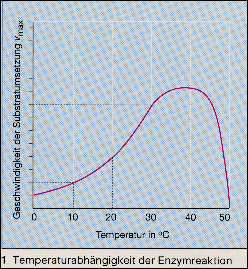
Aufgabe 3: Reaktionsgeschwindigkeit eines Enzyms -Fortsetzung

Bei chemischen Reaktionen zeigt sich, dass sich die Reaktionsgeschwindigkeit eines Enzyms verdoppelt, wenn die Temperatur um etwa 10^o C erhöht wird. Diese Abhängigkeit ist aus der physikalischen Chemie als Reaktionsgeschwindigkeit-Temperatur-Regel (kurz: RGT-Regel) bekannt. Diese Abhängigkeit der Reaktionsgeschwindigkeit von der Temperatur zeigt das folgende Schaubild, das hier näher mathematisch untersucht werden soll:

(Quelle: NATURA. Biologie für Gymnasien.
Stoffwechsel. Klett, Stuttgart 1995, S. 22)

Gesucht sind die Gleichungen zweier ganzrationaler Funktionen F1 und F2 , die zusammengesetzt den Verlauf der Temperaturabhängigkeit einer enzymatischen Reaktion beschreiben, bei der die theoretische Abhängigkeit nach der RGT-Regel mit dem Verlauf der Denaturierung kombiniert ist.
Folgende Tabelle liefert die notwendigen Bedingungen für die Bestimmung der Funktionsgleichungen:

3.1 Stellen Sie zunächst die notwendigen Gleichungen für die Bestimmung der Funktionsgleichung von F1
      auf! F1 soll vereinfachend eine ganzrationale Funktion 3. Grades sein! Sie benötigen die Werte von
      0^o bis 30^o C !
     
3.2 Stellen Sie analog für die Werte von 30^o bis 50^o C die Bedingungen für eine ganzrationale Funktion F2
      4. Grades auf ! Dabei sollen die Kurven zu F1 und F2 "ohne Knick" bei 30^o C zusammenstoßen!
      Das Temperaturoptimum liegt bei 38^o C .

3.3 Die Lösung der zugehörigen Gleichungssysteme für die Bestimmung der Funktionsgleichungen zu F1
      bzw. zu F2 finden Sie nun im DERIVE-File Enzym.mth und ist an dieser Stelle nicht verlangt.
      Zur Lösung mit DERIVE wurde zur Abwechslung ein Weg gewählt, der ohne das konkrete Aufstellen
      der Linearen Gleichungssysteme mit dem Befehl "Solve System" auskommt.