Differentialrechnung - Bestimmung von Funktionsgleichungen |
Baustein 2 - 2(11) |
Aufgaben aus dem Bereich der Physik |
|||
|
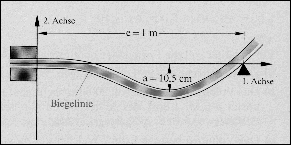
Aufgabe 2: Bestimmung einer Biegelinie
Legt man ein Koordinatensystem wie im Bild,
so kann man die Form des gebogenen Stabes (Biegelinie) rechts
von den Backen näherungsweise durch den Graph einer ganzrationalen
Funktion f 4. Grades angeben. 2.1 Stellen Sie die für
die Bestimmung von f notwendigen Bedingungen auf !
2.2 Stellen
Sie die Biegelinie im Graphikfenster von DERIVE dar! 2.3 Wo hat die Biegelinie
(rechts vom Backen) einen weiteren Wendepunkt? |
|
|
|
|