Übungsaufgaben zur Kontrolle des Lernerfolgs

Koordinatengeometrie - Lineare Funktionen und ihre Graphen

Baustein 3 - 5(5)

Übungsaufgaben zur Kontrolle des Lernerfolgs

Aufgabe 16:
Damit Sie nicht alle Aufgaben abschreiben müssen, können Sie diese Seite auf einem Drucker ausdrucken.

16.1

Gegeben ist die Gerade g: y = 0,5x + 4 .

Welchen Abstand hat der Mittelpunkt der Strecke [PQ] mit P(0 | -1) und Q(6 | 0) zur Geraden g ?

Veranschaulichen Sie zuerst die geometrische Situation durch eine Skizze (auf Papier).
Überlegen Sie eine Lösungsstrategie und benutzen Sie DERIVE .

16.2

Bestimmen Sie die Gleichung der mittelparallelen Geraden ("Mittelparallele") zu den parallelen Geraden g und h, wobei g: 3x + 4y - 12 = 0 und h: 6x + 8y + 9 = 0 gegeben sind.

TIPP: Formen Sie die Geradengleichungen in die übliche Darstellungsform einer Geraden um.

Veranschaulichen Sie zuerst die geometrische Situation durch eine Skizze (auf Papier).
Überlegen Sie eine Lösungsstrategie und benutzen Sie DERIVE!

16.3

Gegeben ist das Dreieck ABC durch A(2 | 2), B(6 | 2) und C(4 | 6).

Berechnen Sie von Hand auf Papier :

-	die Mittelpunkte der Seiten (Bezeichnen Sie dazu die Mittelpunkte mit M₁ für die Seite c, mit M₂ für die Seite a und mit M₃ für die Seite b.),
-	die Gleichungen der Mittelsenkrechten m_a zu a, m_b zu b und m_c zu c,
-	den Schnittpunkt S der Mittelsenkrechten,
-	den Radius r des Umkreises,
-	die Gleichung des Umkreises für das Dreieck ABC.

Rufen Sie danach DERIVE auf und stellen Sie das Dreieck, die Mittelsenkrechten und den Umkreis im Graphikfenster dar.

16.4

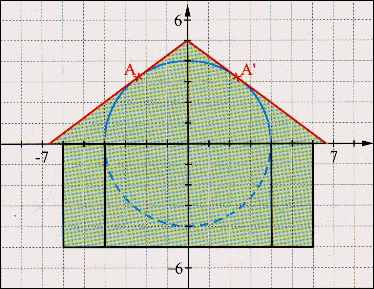
Nebenstehend ist eine Markthalle in Vorderansicht dargestellt. Der große Saal wird von einem Tonnengewölbe überspannt. Das Satteldach liegt auf dem Gewölbe auf und hat eine Neigung von 75%.

(Quelle: Elemente der Mathematik 11. Schuljahr, Nordrhein-Westfalen, Schroedel Verlag, 1999, S. 65)

16.4.1

Geben Sie die Gleichung des eingezeichneten Kreises K an!

16.4.2

Geben Sie für den linken und rechten Dachbalkens je eine Geradengleichung an! (In Wirklichkeit bestimmen Sie die Gleichungen der Unterkanten der Dachbalken.)

16.4.3

Bestimmen Sie von Hand auf Papier die Punkte A und A', bei denen die Balken auf dem Tonnen-gewölbe aufliegen!

16.5

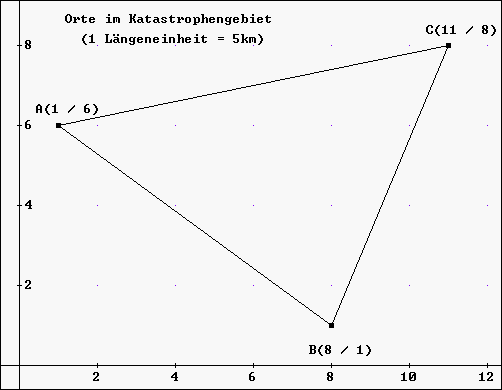
In einem Katastrophengebiet soll eine Rettungszentrale R eingerichtet werden, von der aus die Orte A, B und C mit Hubschraubern versorgt werden sollen. Damit die Hubschrauber möglichst viele Lasten transportieren können, sollen ihre Treibstofftanks nur so weit gefüllt werden, dass ein sicherer Hin- und Rückflug gewährleistet ist. Um R bestimmen zu können, sind die Orte A, B und C in ein Koordinatensystem übertragen worden ( 1 Längeneinheit = 5km):

(Die Aufgabe ent-stammt: Mathematik 11. Schuljahr, Cornelsen Verlag, Berlin 2000, S.50)

Wo soll die Rettungszentrale R eingerichtet werden?

Berechnen Sie von Hand unter Zuhilfenahme eines Taschenrechners die genaue Lage der Rettungszentrale R
und bestimmen Sie dann mit DERIVE die Entfernungen zwischen R und den Orten A, B und C.
Wie viele km müssen die Hubschrauber fliegen?
Veranschaulichen Sie auch die Situation im Graphikfenster von DERIVE !

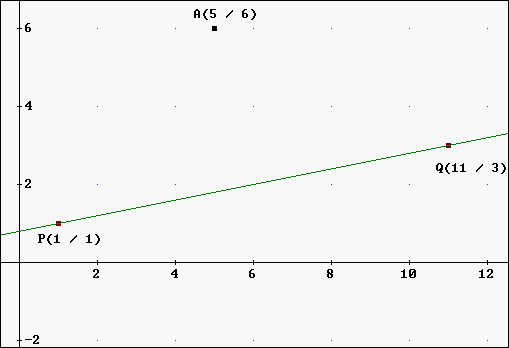
16.6

Durch zwei Punkte P(1 | 1) und Q(11 | 3) ist eine Gerade g gegeben (siehe unten). Der Punkt A(5 | 6) soll an der Geraden g gespiegelt werden:

(Die numerischen Grundlagen zu dieser Aufgabe entstammen: Mathematik 11. Schuljahr, Cornelsen Verlag Berlin 2000, S. 50)

Bestimmen Sie die Koordinaten des Spiegelpunkts A' von A!
Bestimmen Sie dazu:
1. Die Gleichung der Geraden g durch P und Q (von Hand auf Papier);

2. die Gleichung der zu g orthogonalen Geraden h durch A (von Hand auf Papier);

3. den Schnittpunkt M der Geraden g mit der Geraden h mit DERIVE ;

4. den Kreis K um M mit Radius r = [AM] (mit DERIVE );

5. den Schnittpunkt A' von h mit K (mit DERIVE ) !

6. Zeichnen Sie dann A, A', g, h und K im Graphikfenster von DERIVE !