|
Viele natürliche Ressourcen wie z. B. Fisch-
oder Waldbestände erneuern sich von selbst. Waldbesitzer oder
Fischzüchter möchten aber einen möglichst großen
Ertrag erwirtschaften. Dabei ist darauf zu achten, dass sie nicht
zu viel Holz schlagen oder zu viele Fische der Zucht entnehmen.
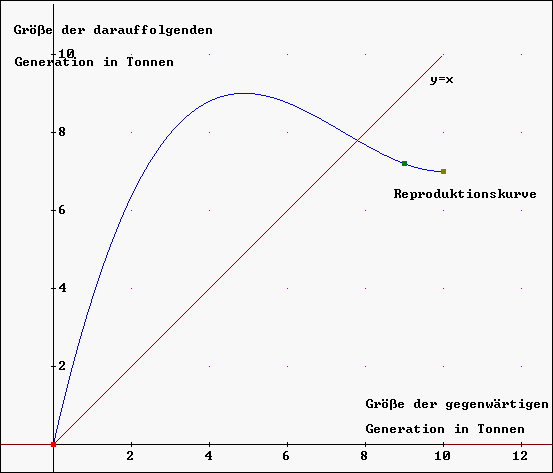
Unten ist nun eine sogenannte Reproduktionskurve
einer Art abgebildet. Sie ist der Graph einer Funktion
f, die der Populationsgröße der gegenwärtigen Generation
die Populationsgröße der darauffolgenden Generation zuordnet.
Auch wenn diese Kurve von Art zu Art variiert, so hat sie unter
vernünftigen biologischen Annahmen immer eine ähnliche
Form wie die abgebildete Reproduktionskurve für einen Fischbestand.
Bei einer wirtschaftlichen Nutzung des Fischbestands versucht der
Züchter nun, jährlich eine möglichst konstante Entnahme
E zu tätigen. Da die Fischpopulation in einem Jahr von x auf
f(x) zunimmt, beträgt dann der natürliche Zuwachs f(x)
- x. Daher wird eine konstante Entnahme E erreicht, wenn gilt:
E = f(x) - x.
(a) Bestimmen Sie mit Hilfe
von DERIVE die Gleichung der Reproduktionskurve f unter Beachtung
folgender Tabelle ( f soll eine ganzrationale Funktion 3. Grades
sein):
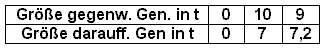
Beachte: Für 10 Tonnen liegt ein lokales Extremum vor!
(b) Bestimmen Sie mittels DERIVE
das Maximum (in t) der Entnahme E, die der Züchter dem
Bestand entnehmen darf ! Wie groß (in t) darf also die Population
werden?
Minimieren Sie dazu den Internet Browser (oben rechts, linker Button)
und rufen Sie das Programm DERIVE auf ! Kehren Sie danach
wieder in den Lehrgang zurück!
|