Differentialrechnung - Bestimmung von Funktionsgleichungen |
Baustein 2 - 10(11) |
Aufgaben aus dem Bereich des Alltags |
|
|
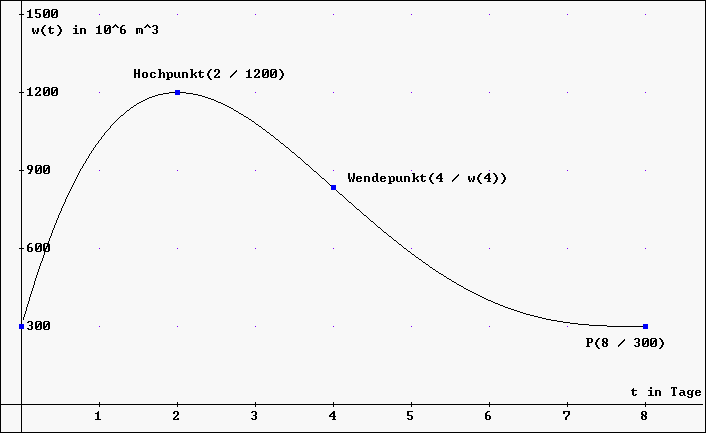
Aufgabe 1: Hochwasser Ein Fluss transportiere normalerweise 300·106 m3 Wasser täglich. Durch anhaltende Regenfälle kommt es zum Hochwasser. Folgender Graph zeigt näherungsweise den Verlauf des Hochwassers:
1.1 Beschreiben Sie mit eigenen Worten den zeitlichen Verlauf des Hochwassers!
Bestimmung des Funktionsterms w(t) (t = Anzahl der Tage) einer ganzrationalen Funktion w vierten Grades, die die "Hochwasserkurve" als Graph besitzt: 1.3 Bestimmen Sie die notwendigen
Bedingungen für w(t) aus dem Graphen und stellen Sie das
1.4 Lösen Sie das zugehörige lineare
Gleichungssystem mit DERIVE und geben Sie die Funktions- |
|
|
|