Aus den fünf Informationen des Graphen zu w und dem Ansatz für w ergibt sich folgendes lineare Gleichungssystem mit 5 Gleichungen und 5 Unbekannten, dass nun mit DERIVE gelöst werden soll:

   (1) e = 300
   (2) 4096a + 512b + 64c + 8d + 300 = 300
   (3) 16a + 8b + 4c + 2d + 300 = 1200
   (4) 32a + 12b + 4c + d = 0
   (5) 192a + 24b + 2c = 0

DERIVE liefert als Lösung dieses Gleichungssystems:
(Dazu verwendet man entweder den Befehl SOLVE([W(0)=300,W(8)=300,...],[a,b,c,d,e]) oder man verwendet den Befehl Solve > System. In letzterem Fall ist es sinnvoll nur die Gleichungen (2) bis (5) zu betrachten, da man sich so Schreibarbeit ersparen kann.)

Daher ergibt sich als gesuchte Funktionsgleichung für w:

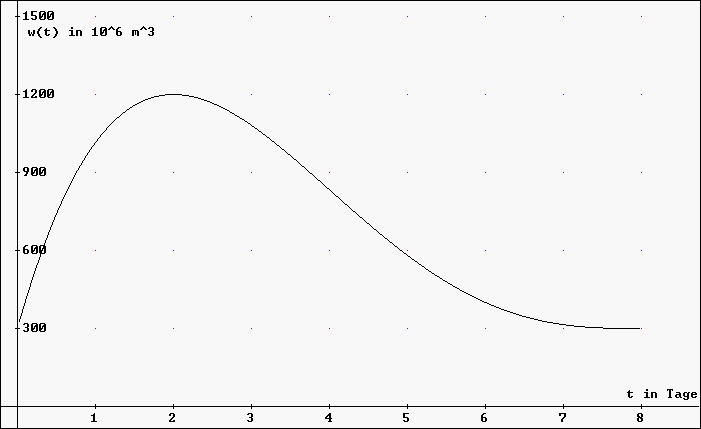
Um nun den Graphen zu w im Bereich 0 £ t £ 8 zu zeichnen, verwendet man die CHI-Funktion.
Die Berechnungen hierzu finden Sie im DERIVE-File "Hochwasser.mth" im Anhang!