----------------------------------------
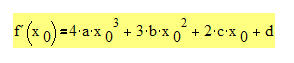
Navigation: Seite zurück und Seite vor
Betrachten wir unser letztes Ergebnis:
Halten wir fest: Für die Funktionen der Form f(x) = ax4+bx³+cx²+dx+e ist die Steigung(sfunktion):
----------------------------------------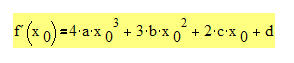
Wir erkennen, dass der Grad sich systematisch reduziert. Aus a•x4 wird 4a•x0³. Der alte Exponent wird als Faktor davor gesetzt und der Grad um 1 reduziert.
Der Faktor a bleibt als Konstante erhalten.
Nach diesem Muster kann jeder Summand bearbeitet werden.
Wir haben damit die ersten drei Regeln erarbeitet.
| Potenzregel | Faktorregel | Summenregel |
| f(x) = xn | f(x)=a•g(x) | f(x)=g(x)+h(x) |
| f´(x)=n•xn-1 | f´(x)=a•g´(x) | f´(x)=g´(x)+h´(x) |
Zuammenfassung mit Beispielen.
Diese Regeln sind noch zu beweisen. (am Beispiel der Summenregel)
Üben Sie:
1.) f(x) = x5
2.) f(x) = 3x6
3.) f(x) = -4x6 +3x5
Hier eine Wiederholung.
weiter Übungsaufgabe!!! (Lösungen)
Wichtig: Spätestens jetzt sollten Sie noch einmal alle wichtigen Lösungesverfahren wiederholen, die das Lösen von Gleichungen höheren Grades ermöglichen. Erinnert sei an die Substituion, eine Lösung finden mit anschließender Polynomdivision und nicht zuletzt an den Satz vom Nullprodukt.
Wiederholen Sie!!!! (siehe auch bei sos-mathe.ch)