| Station 13 | Polynomdivision | JJ | G |
Gegeben ist die quadratische Funktion f(x):= x² - 5x + 6.
Erster Rückgriff auf euer Vorwissen:
Bestimme die Nullstellen von f und löse die Klammern auf: (x-2) . (x-3)!
Beobachtungen:
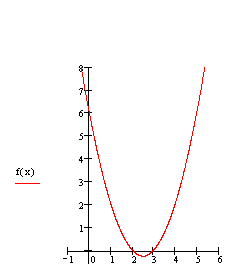
1. f(x) = x² - 5x + 6
= (x-2) . (x-3), wobei 2 und 3 die beiden Nullstellen von f sind.
2. Die Faktoren (x – 2) und (x -3) nennt man Linearfaktoren des Funktionsterms f(x) = x² - 5x + 6.
3. Die Nullstellen 2 und 3 sind Teiler von 6 in dem Funktionsterm von f(x).
Zweiter Rückgriff auf euer Vorwissen:
Es gilt: 144 = 6 . 24.
Dann gilt auch: 144 : 6 = 24.
Kann man dies auch auf Terme
übertragen? Konkret:
Es gilt: x² - 5x + 6 = (x-2) .
(x-3).
Gilt dann wie bei der "normalen" Division (x² - 5x + 6) : (x
– 2) = (x-3)?
Bearbeite zur Vorbereitung dieser Überlegung die folgende
Aufgabe1:
Führe die Division 144 : 6 schriftlich durch!
Übertrage die schriftliche Division auf die Division (x² - 5x + 6) : (x – 2):
(x² - 5x + 6) : (x – 2)
= x – 3
Begründung:
-(x² - 2x)
x . (x – 2) = x² - 2x
-
3x + 6
x² - x² = 0 und -5x – (-2x) = -5x + 2x = -3x, und
"+ 6" unten hinschreiben
-(-
3x + 6)
-3 . (x – 2) = -3x + 6,
0
-3x + 6 –(-3x + 6) = 0
Es gilt also: x² -5x + 6 = (x - 2) . (x – 3)!
Hinweise:
- Diese Art von Division nennt man Polynomdivision.
- Wenn man eine Polynomdivision durchführen soll, muss man aber eine Nullstelle des Divisors kennen!
- Mit Hilfe der Polynomdivision kann man Funktionsgleichungen in Linearfaktoren zerlegen.
Gegeben ist nun die Funktion f mit f(x) = x³ - 15x² + 71x - 105, deren Funktionsgraph unten zu sehen ist:
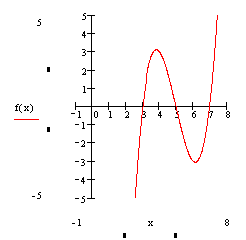
f hat die Nullstellen 3, 5 und 7.
Aufgabe 2:
Zerlege f(x) = x³ - 15x² + 71x
- 105 mit Hilfe der Polynomdivision
in Linearfaktoren!
Aufgabe 3:
Zerlege die Funktion f(x) = x³ - 2x² - x + 2 mit der Polynomdivision in Linearfaktoren!
Hinweis: Fertige keine Zeichnung an. Suche die erste Nullstelle unter den Teilern von +2!
Warum sollen die Teiler von 2 gesucht werden?
Polynomdivision und Zerlegung in Linearfaktoren
| zurück |

