Symmetrie von ganzrationalen Funktionen
Während die Graphen von quadratischen Funktionen und Potenzfunktionen relativ leicht zu zeichnen und zu erkennen sind, lassen sich Funktionen höheren Grades nicht so leicht erfassen bzw. skizzieren. Es lohnt sich daher, einige Erfahrungen im Umgang mit ganzrationalen Funktionen zu sammeln und den Verlauf ihrer Graphen zu untersuchen.
Aufgabe 1
Betrachte die folgenden ganzrationalen Funktionen.
a) Was fällt dir hinsichtlich der Symmetrie der Funktionsgraphen auf?
b) Berechne für beide Funktionen jeweils f(1), f(-1), f(2), f(-2), f(3) und f(-3).
c) Berechne auch f(a) und f(-a). Vergleiche die Ergebnisse.
d) Wie lässt sich rechnerisch nachweisen, dass eine Funktion zur y-Achse symmetrisch ist?
Aufgabe 2
Betrachte nun die Graphen der folgenden Funktionen .
a) Sind diese Graphen auch symmetrisch? Wenn ja, welche Art von Symmetrie liegt vor?
b) Berechne auch hier jeweils f(1), f(-1), f(2), f(-2), f(3) und f(-3).
c) Vergleiche f(a) und f(-a).
d) Formuliere einen Satz, wann eine Funktion punktsymmetrisch zum Ursprung ist.
Aufgabe 3
Ist es möglich, bei einer beliebigen ganzrationalen Funktion ohne Rechnung Aussagen zur Symmetrie zu machen ?
Probier doch einfach aus, ob du anhand des Funktionsterms voraussagen kannst, ob die Funktion achsensymmetrisch zur y-Achse oder punktsymmetrisch zum Ursprung ist.
Bei dem nachfolgenden Programm kannst du die vorgegebene Funktion beliebig verändern und untersuchen, inwieweit die Funktion symmetrisch ist. Probiere verschiedene Funktionen aus und beantworte folgende Fragen.
a) Wie muss eine ganzrationale Funktion beschaffen sein, damit sie achsensymmetrisch zur y-Achse ist?
b) Wie muss sie beschaffen sein, damit sie punktsymmetrisch zum Ursprung ist?
Aufgabe 4
Nachdem du nun weißt, wann eine ganzrationale Funktion auf jeden Fall symmetrisch ist, solltest du die folgenden Funktionen auch rechnerisch noch einmal auf Symmetrie untersuchen.
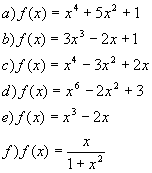
Hast du bemerkt, dass du auch eine nicht ganzrationale Funktion untersucht hast?
