Differentialrechnung - Bestimmung von Funktionsgleichungen |
Baustein 2 - 4(11) |
Aufgaben aus dem Bereich der Biologie |
|
|
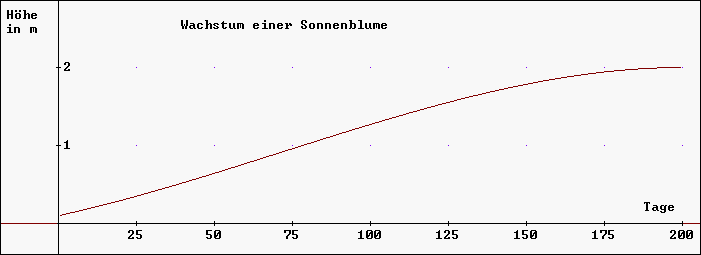
Wird die Höhe einer Sonnenblume während des Wachsens
gemessen, so erhält man ungefähr einen Verlauf wie in
untenstehendem Schaubild: 2.1 Gesucht ist die Funktionsgleichung einer
ganzrationalen
Funktion
f 3. Grades, die die
oben 2.2 Lösen Sie das gefundene Gleichungssystems
mit DERIVE ! Minimieren Sie dazu den
Internet Browser (oben rechts, linker Button) und rufen Sie das
Programm
DERIVE auf ! Kehren Sie danach wieder in den
Lehrgang zurück! 2.3 Zu welchem Zeitpunkt wuchs die Sonnenblume
am stärksten? 2.4 Nach wievielen Tagen war die Sonnenblume
genau 1,00 m hoch? Nach wievielen Tagen genau 1,50m? |
|
|
|
|