| Station 6 | Codierung von Nachrichten |  |
Gelegentlich
verschlüsselt man Nachrichten, um sie vor einem Missbrauch durch
Unbefugte zu schützen. Eine Möglichkeit Nachrichten so zu codieren,
dass sie von Unbefugten nicht ohne weiteres verstanden werden können,
vom Empfänger jedoch eindeutig zu entschlüsseln sind, ist die
im folgenden beschriebene.
Allen Buchstaben des Alphabets werden Zahlen zugeordnet, z.B.:
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | Leer |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |
22 15 18 19 9 3 8 20 27 22 5 18 19 3 8 12 21 5 19 19 5 12 20
Diese Matrix kann
man mit einer sogenannten Codiermatrix C multiplizieren und erhält
eine verschlüsselte Nachricht:
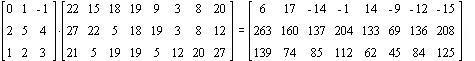
Aus der obigen Zahlenfolge ist also die folgende verschlüsselte Zahlenfolge geworden:
6 17 -14 -1 14 -9 -12 -15 263 160 137 204 . . .
Als legitimer Empfänger dieser codierten Nachricht muss man natürlich die Möglichkeit haben, den Prozess der Verschlüsselung rückgängig zu machen, also eine Matrix zu bestimmen, mit der man zu der ursprünglichen Zahlenfolge zurück kommt, die also diese Transformation rückgängig macht..
Eine Matrix, die
an der ursprünglichen Zahlenfolge nichts ändert, ist die sogenannte
Einheitsmatrix 
.
Gesucht ist folglich eine Matrix, die multipliziert mit mit der Matrix
C die Einheitsmatrix ergibt. Diese zu C inverse
Matrix bezeichnet man mit C -1 . Man berechnet
C -1, indem man die Matrix C in die Einheitsmatrix umformt
und dabei simultan die gleichen elementaren Umformungen auf die Einheitsmatrix
anwendet:
Zeile III wird zu Zeile I , Zeile I wird zu Zeile II ,
Zeile II wird zu Zeile III
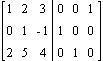III
+ (-2) I
III
+ (-1) II und III (-1)
I
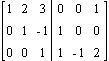+ (-3) III und II + III
I
+ (-2) II
Aufgabe 1:
(a) Prüfen Sie für die 1. Spalte der Matrix
der verschlüsselten Nachricht, ob sie mithilfe der inversen Matrix
wieder entschlüsselt werden kann.
(b) Codieren
Sie das Wort "NORMAL"
(c) Der Empfänger sendet die folgende Zahlenfolge
zurück.
14 13 3 -9 231 104 147 222 115 46 78 129
Decodieren Sie die Nachricht.
Aufgabe 2:
Bestimmen Sie zu den folgenden Codiermatrizen jeweils die Decodiermatrizen.
(a) 
(b) 
Aufgabe 3:
Müssen Matrizen, die zum Codieren von Informationen in Frage kommen,
Bedingungen erfüllen oder kann man mit jeder quadratischen Matrix
Informationen eindeutig - also umkehrbar eindeutig - codieren ?
| zurück |
