| Station
7 |
Geometrische Abbildungen in der Ebene |
![]()
![]()
Bei der Programmierung
von Computergrafiken wird sehr oft auf die Abbildungsgeometrie zurückgegriffen.
Zweidimensionale Objekte können durch geometrische Abbildungen bewegt
oder verzerrt werden. Die grafische Darstellung von dreidimensionalen
Objekten auf dem Bildschirm wird mit Hilfe von Projektionsabbildungen
erzeugt. Auch die optische Veranschaulichung von Bewegungen dieser Objekte
wird durch geometrische Abbildungen erreicht.
Bei geometrischen
Abbildungen wird jedem Punkt P(x1|x2) ein Bildpunkt P'(x'1|x'2)
zugeordnet. Der Zusammenhang zwischen Punkt und Bildpunkt lässt sich
durch Abbildungsgleichungen beschreiben.
Beispiel 1
Spiegelung an der x-Achse
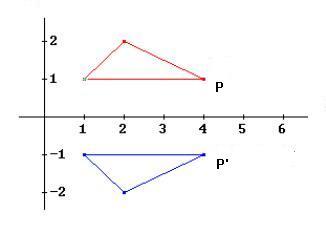 |
Die
Abbildungsgleichungen lauten: x'1= x1 x'2= - x2 |
Beispiel 2
Zentrische Streckung vom Ursprung aus mit dem Faktor 2
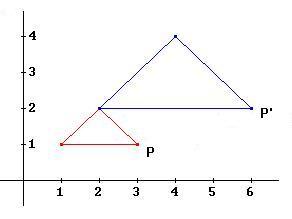 |
Die
Abbildungsgleichungen lauten:
|
Um den Zusammenhang
zwischen dem Ortsvektor zum Punkt P und dem Ortsvektor zu seinem Bildpunkt
P' übersichtlicher als in den Abbildungsgleichungen darzustellen,
kann man den Ortsvektor des Bildpunktes P' als Produkt einer Abbildungsmatrix
A und dem Ortsvektor des Punktes P schreiben.
Die Abbildungen der obigen Beispiele können dann folgendermaßen
dargestellt werden:
|
Koordinatendarstellung
|
Matrixdarstellung
|
|
| Beispiel 1 |
|
|
| Beispiel 2 |
|
|
Für die
Matrixdarstellung der Abbildungen gilt::
|
Eine
lineare Abbildung eines Punktes P mit dem Ortsvektor
beschrieben werden.
|
Aufgabe 1
Eine lineare Abbildung ist durch ihre Abbildungsmatrix M gegeben. Bestimmen
Sie die Koordinaten der Bildpunkte des Dreiecks ABC. Zeichnen Sie Ausgangsdreieck
und Bilddreieck in ein Koordinatensystem ein. Welche Abbildung wird durch
die Matrix M beschrieben?
| a) | A(2|3), B(3|4), C(-1|4) | |
| b) | A(1|0), B(-2|3), C(0|4) | |
| c) | A(1|-3), B(3|-2), C(5|0) |
Eine lineare Abbildung ist durch ihre Abbildungsmatrix M gegeben. Bestimmen
Sie die Koordinaten der Bildvektoren der sogenannten Einheitsvektoren.
Was stellen Sie fest?
a) 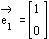
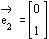
b) 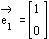
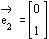
c) 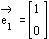
| zurück |

