Differentialrechnung - Bestimmung von Funktionsgleichungen |
Lösung |
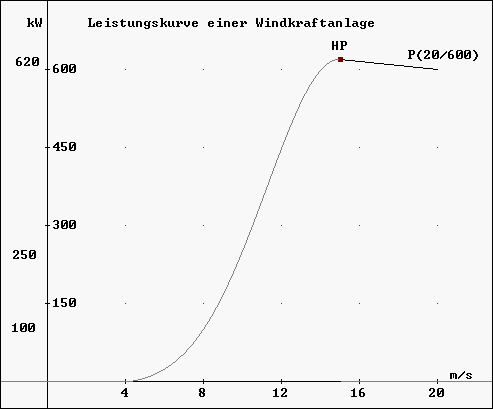
Leistungskurve einer Windkraftanlage: Lösung zu Aufgabe 1.2
f(x) = a·x6 + b·x5 + c·x4 + d·x3 + e·x2 + g·x+ h wobei a, b, c, d, e, g, hÎ IR.f '(x) = 6·a·x5 + 5·b·x4 + 4·c·x3 + 3·d·x2 + 2·e·x + g
Die 7 Bedingungen (Gleichungen), die sich aus der Kurve ergeben, sind:
| (1) f(4) = 0 | Û | a·46 | + b·45 | + c·44 | + d·43 | + e·42 | + g·4 | + h | = 0 |
| (2) f '(4) = 0 | Û | 6·a·45 | + 5·b·44 | + 4·c·43 | + 3 ·d ·42 | + 2 ·e ·4 | + g | = 0 | |
| (3) f(8) = 100 | Û | a ·86 | + b ·85 | + c ·84 | + d ·83 | + e ·82 | + g ·8 | + h | = 100 |
| (4) f(10) = 250 | Û | a ·106 | + b ·105 | + c ·104 | + d ·103 | + e ·102 | + g ·10 | + h | = 250 |
| (5) f(15) = 620 | Û | a ·156 | + b ·155 | + c ·154 | + d ·153 | + e ·152 | + g ·15 | + h | = 620 |
| (6) f '(15) = 0 | Û | 6 ·a ·155 | + 5 ·b ·154 | + 4 ·c ·153 | + 3 ·d ·152 | + 2 ·e ·15 | + g | = 0 | |
| (7) f(20) = 600 | Û | a ·206 | + b ·205 | + c ·204 | + d ·203 | + e ·202 | + g ·20 | + h | = 600 |
Entweder benutzt man zur Lösung dieses Gleichungssystems den Befehl SOLVE > SYSTEM (was hier sehr mühsam ist) oder man benutzt den SOLVE-Befehl sofort:
SOLVE([F(4)=0, F'(4)=0, F(8)=100, F(10)=250, F(15)=620, F'(15)=0, F(20)=600],[a,b,c,d,e,g,h]) .
DERIVE liefert nun als Lösung:

Mittels der CHI-Funktion lässt sich dann der zugehörige Graph im Bereich [4; 15] im Graphikfenster von DERIVE veranschaulichen mittels der Befehlszeile CHI(4,x,15)*F(x) , die dann nur noch berechnet werden muss (vgl. DERIVE-File Windkraft.mth ). Im Intervall [15; 20] muss allerdings ein Geradenstück gezeichnet werden.
|
|
|