Leistungskurve einer Windkraftanlage: Hilfe 2 zu Aufgabe 1.2

Der Ansatz für eine ganzrationale Funktion 6. Grades lautet:

f(x) = a·x⁶ + b·x⁵ + c·x⁴ + d·x³ + e·x² + g·x+ h
wobei a, b, c, d, e, g, h Î IR .

(Auf die Verwendung des Parameters f wird hier verzichtet, da das Computer-Algebra-System DERIVE
f im Allgemeinen mit einer Funktion identifiziert.)

Für f '(x) ergibt sich dann:

f '(x) = 6·a·x⁵ + 5·b·x⁴ + 4·c·x³ + 3·d·x² + 2·e·x + g

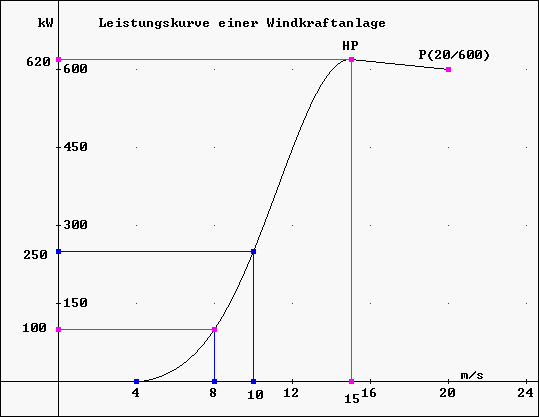
Die 7 Bedingungen (Gleichungen), die sich aus der Kurve ergeben, sind:

(1) f(4) = 0 (2) f '(4) = 0 (3) f(8) = 100 (4) f(10) = 250 (5) f(15) = 620 (6) f '(15) = 0 (7) f(20) = 600