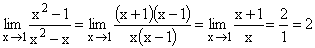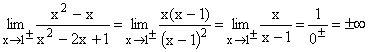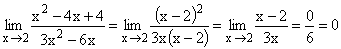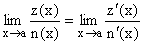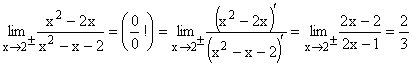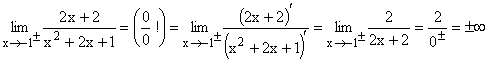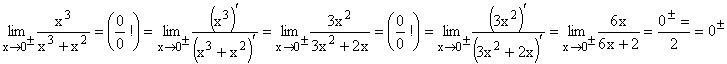So, nun geht es los.
Allgemein unterscheidet man bei Grenzwerten solche, bei denen x gegen schon viel größer als 1002 und (-100)5 betragsmäßig
ebenfalls viel größer als (-100)3 .
Im folgenden werden die obigen drei Beispiele nochmal aufgegriffen:
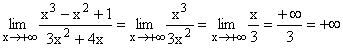 |
Im Zähler werden alle Potenzen von x unter 3 und im Nenner alle unter 2 weggelassen und dann x3 gekürzt. Danach ergibt sich der klare Grenzwert: Unendlich/Zahl
Gf hat eine schräge Asymptote da der Zählergrad 3 um eins höher ist als der Nennergrad 2. |
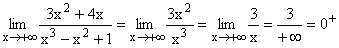 |
Nach Weglassen der niedrigeren Potenzen im Zähler und Nenner und Kürzen ergibt sich der klare Grenzwert: Zahl/Unendlich
Gf hat die waagrechte Asymptote y=0 mit Annäherung nur von oben her. |
 |
Nach Weglassen der niedrigeren Potenzen im Zähler und Nenner und Kürzen ergibt sich der klare Grenzwert 3
Gf hat die waagrechte Asymptote y=3 . |
3) Rechnerische Lösung
Prinzip:
Man klammert die höchste Potenz des Nenners oder Zählers aus (einfacher ist das
Ausklammern beim Nenner), kürzt dann und benutzt die Tatsache, dass alle
Summanden der Form 1/x , 1/x2 usw. für x gegen Unendlich dann gegen Null gehen.
Folgendes Beispiel zeigt diese Prinzip:
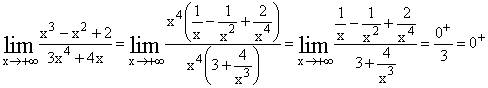
0+ deshalb, weil die Terme 1/x2 und 2/x4 im Zähler für große
x gegenüber dem Term 1/x zu vernachlässigen sind (probiere es mit dem
Taschenrechner aus).
4) Allgemeine Merkregel
Auf Grund des Weglassen-Prinzips und auch wegen der rechnerischen Lösung ergibt sich eine leicht anwendbare Merkregel für die Grenzwerte x gegen Unendlich.
Ist f(x) eine rationale Funktion der Form:
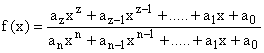 |
so gilt: |
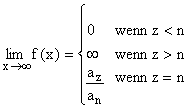 |
Die Vorzeichen von Null und Unendlich ergeben sich aus den Koeffizienten az und an der höchsten Potenzen von Zähler und Nenner und dadurch, ob diese Potenzen gerade oder ungerade sind.
II. Grenzwerte für x ® Zahl
1) Klare Grenzwerte
Wird der nur Zähler oder nur der Nenner Null, wenn man diese Zahl einsetzt, so ergibt sich auf jeden Fall ein klarer Grenzwert der Form 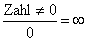 oder
oder 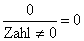 .
.
Die folgenden zwei Beispiele zeigen diese Möglichkeiten:
2) Unklarer Grenzwert 0/0 - Faktorisieren
Problematisch bei dieser Grenzwertbildung ist es nur, wenn diese Zahl gleichzeitig eine Nullstelle des Zählers und Nenners ist. Dann ergibt sich nämlich der unklare Grenzwert 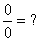 Durch Zerlegen von Zählerpolynom und Nennerpolynom kann die gemeinsame Nullstelle aber bestimmt und dann gekürzt werden, so dass aus dem unklaren Grenzwert ein klarer Grenzwert entsteht, da ja nach dem Kürzen entweder Zähler oder Nenner oder beide bei der Grenzwertbildung nicht mehr Null werden.
Durch Zerlegen von Zählerpolynom und Nennerpolynom kann die gemeinsame Nullstelle aber bestimmt und dann gekürzt werden, so dass aus dem unklaren Grenzwert ein klarer Grenzwert entsteht, da ja nach dem Kürzen entweder Zähler oder Nenner oder beide bei der Grenzwertbildung nicht mehr Null werden.
Folgende Beispiele zeigen dieses Verfahren:
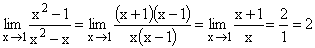 |
Zerlegen von Zähler und Nenner ergibt
die gemeinsame Nullstelle 1 , die dann vollständig gekürzt werden
kann.
Gf hat bei x=1 eine stetig behebbare Definitionslücke.
|
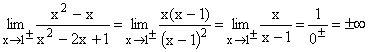 |
Die gemeinsame Nullstelle 1 bleibt im
Nenner auch nach dem Kürzen übrig, aber es entsteht der
klare Grenzwert Zahl/0 .
Gf hat bei x=1 eine senkrechte Asymptote .
|
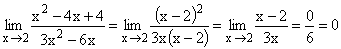 |
Die gemeinsame Nullstelle 2 bleibt im
Zähler auch nach dem Kürzen übrig, aber es entsteht der
klare Grenzwert 0/Zahl .
Gf hat bei x=2 eine stetig behebbare Definitionslücke.
|
3) Unklarer Grenzwert 0/0 - Regel von de l'Hospital
Für solche, die nicht gerne Faktorisieren (obwohl man dies ja eigentlich sowieso im Zähler für die Nullstellen und im Nenner für die Definitionsmenge tun muss) ist die Regel von de l'Hospital (sprich: delopital) eine schöne Möglichkeit für Grenzwerte der Form 0/0.
| Sie lautet vereinfacht für diesen Fall: |
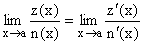 |
Das bedeutet:
Leite Zähler und Nenner jeweils für sich und unabhängig voneinander ab und zwar solange, bis aus dem unklaren Grenzwert 0/0 ein klarer Grenzwert wird.
Du kannst also auch öfter als einmal ableiten, aber immer bei Zähler und Nenner gleichzeitig und unabhängig voneinander.
Folgende drei Beispiele zeigen diese Regel:
| 1. |
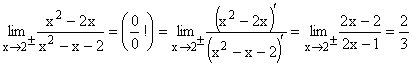
|
| |
Bei Einsetzen von 2 ergibt sich zunächst der unklare Grenzwert 0/0 . Leitet man Zähler und Nenner je für sich einmal ab, dann kommt der klare Grenzwert 2/3 heraus.
Gf hat bei x=2 eine stetig behebbare Definitionslücke.
|
| 2. |
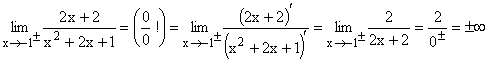
|
| |
Bei Einsetzen von -1 ergibt sich zunächst der unklare Grenzwert 0/0 . Leitet man Zähler und Nenner je für sich einmal ab, dann kommt der klare Grenzwert Zahl/0 = ¥ heraus.
Gf hat bei x=2 eine senkrechte Asymptote.
|
| 3. |
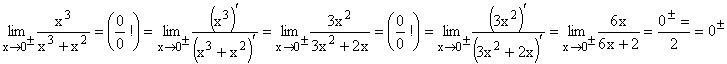
|
| |
Bei Einsetzen von 0 ergibt sich zunächst der unklare Grenzwert 0/0 . Leitet man Zähler und Nenner je für sich einmal ab, dann kommt wieder derselbe unklare Grenzwert heraus. Erst durch nochmaliges getrenntes Ableiten ergibt sich der klare Grenzwert 0/Zahl = 0 heraus.
Gf hat bei x=0 eine eine stetig behebbare Definitionslücke.
|
So, das war's schon mit den Grenzwerten bei rationalen Funktionen.
Wenn du mehr zum Thema Grenzwertbildung wissen willst, so arbeite den Crashkurs Grenzwertbestimmung
durch, den du bald auch auf diesen Seiten findest.
Du kannst dir auch hier die Offline-Version dieses Crash-Kurses als selbstentpackendes ZIP-File herunterladen.
Noch ein letztes Wort in eigener Sache:
Nobody is perfect und auch ich bin es nicht. Sollten auf diesen Seiten mathematische - oder Schreibfehler sein, so maile dies doch bitte an die folgende Adresse:
org.postmaster@wvsg.schulen.regensburg.de
Kurt Brühmann, 25.9.2003
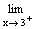 heißt: x ist bei der Annäherung größer als 3, also z.B. 3,1 ; 3,01 ; 3,001 usw
heißt: x ist bei der Annäherung größer als 3, also z.B. 3,1 ; 3,01 ; 3,001 usw
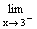 heißt: x ist bei der Annäherung kleiner als 3, also z.B. 2,9 ; 2,99 ; 2,999 usw
heißt: x ist bei der Annäherung kleiner als 3, also z.B. 2,9 ; 2,99 ; 2,999 usw
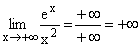 einverstanden.
einverstanden. 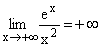
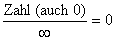 in Frage.
in Frage.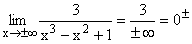
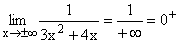
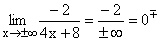
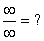 in Frage, da ja das Zählerpolynom und das Nennerpolynom beide gegen Unendlich gehen.
Folgende drei Beispiele zeigen, dass je nach Funktion völlig unterschiedliche Ergebnisse entstehen können.
in Frage, da ja das Zählerpolynom und das Nennerpolynom beide gegen Unendlich gehen.
Folgende drei Beispiele zeigen, dass je nach Funktion völlig unterschiedliche Ergebnisse entstehen können.
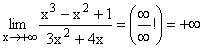
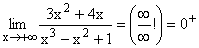
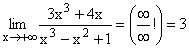
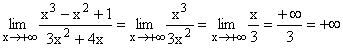
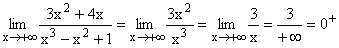

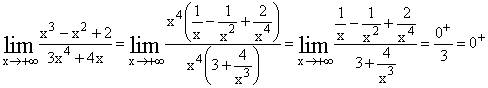
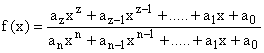
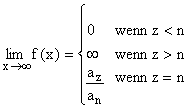
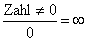 oder
oder 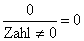 .
. 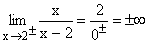
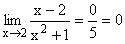
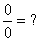 Durch Zerlegen von Zählerpolynom und Nennerpolynom kann die gemeinsame Nullstelle aber bestimmt und dann gekürzt werden, so dass aus dem unklaren Grenzwert ein klarer Grenzwert entsteht, da ja nach dem Kürzen entweder Zähler oder Nenner oder beide bei der Grenzwertbildung nicht mehr Null werden.
Durch Zerlegen von Zählerpolynom und Nennerpolynom kann die gemeinsame Nullstelle aber bestimmt und dann gekürzt werden, so dass aus dem unklaren Grenzwert ein klarer Grenzwert entsteht, da ja nach dem Kürzen entweder Zähler oder Nenner oder beide bei der Grenzwertbildung nicht mehr Null werden.