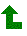
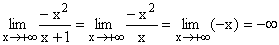
Gf hat eine schräge Asymptote , da der Zählergrad um 1 höher ist, als der Nennergrad.
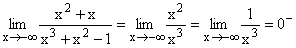
Gf hat die waagrechte Asymptote y=0 .
Gf hat die waagrechte Asymptote y=3/2 .
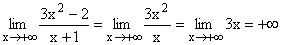
Gf hat eine schräge Asymptote da der Zählergrad um 1 höher ist, als der Nennergrad.
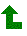 |
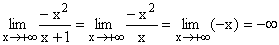 |
Nach Weglassen von 1 im Nenner und Kürzen bleibt -x
übrig.
Gf hat eine schräge Asymptote , da der Zählergrad um 1 höher ist, als der Nennergrad. |
 |
Nach Weglassen von x im Zähler und x2 -1 im
Nenner und Kürzen bleibt 1/x3 übrig.
Gf hat die waagrechte Asymptote y=0 . |
|
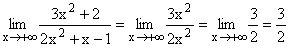 |
Nach Weglassen von 2 im Zähler und x -1 im Nenner und
Kürzen bleibt 3/2 übrig.
Gf hat die waagrechte Asymptote y=3/2 . |
|
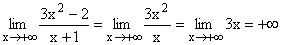 |
Nach Weglassen von 2 im Zähler und 1 im Nenner und
Kürzen bleibt 3x übrig.
Gf hat eine schräge Asymptote da der Zählergrad um 1 höher ist, als der Nennergrad. |
| 1.Bsp | 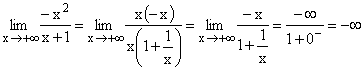 |
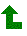 |
Nach Ausklammern von x im Zähler und Nenner und Kürzen,
geht der Nenner gegen 1, der Zähler gegen -¥ .
Gf hat eine schräge Asymptote , da der Zählergrad um 1 höher ist, als der Nennergrad.
|
| 2.Bsp | 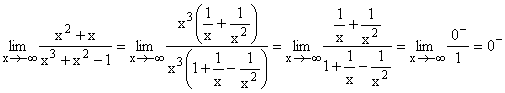 |
| Nach Ausklammern von x3 im Zähler und Nenner und Kürzen,
geht der Nenner gegen 1, der Zähler gegen 0- (Minus, weil
1/x negativ ist und 1/x2 für große negative x
vernachlässigt werden kann).
Gf hat die waagrechte Asymptote y=0 .
|
|
| 3.Bsp | 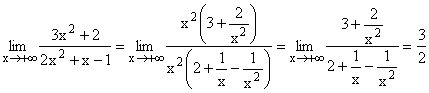 |
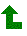 |
Nach Ausklammern von x2 im Zähler und Nenner und Kürzen,
geht der Nenner gegen 2 und der Zähler gegen 3 da alle Terme 1/x und 1/x2 gegen 0 gehen.
Gf hat die waagrechte Asymptote y=3/2 .
|
| 1.Bsp | 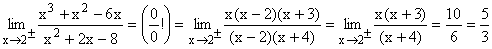 |
 |
Nach Faktorisieren von Zähler und Nenner läßt sich der Faktor x - 2 vollständig herauskürzen und es ergibt sich der einfache Grenzwert 5/3. Dies bedeutet, dass die Stelle x = 2 eine stetig behebbare Definitionslücke von f(x) ist. |
| 2.Bsp | 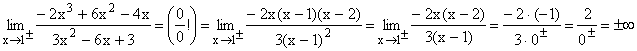 |
| Nach Faktorisieren von Zähler und Nenner läßt sich der Faktor x - 1 nur im Zähler vollständig herauskürzen und es ergibt sich der klare Grenzwert +/-¥.. Bei Annäherung an die Stelle 1 ist zu beachten, von welcher Richtung man gegen 1 geht. Bei Annäherung von rechts her ( 1+ ) bleibt x - 1 stets positiv, es ergibt sich also 0+ , bei Annäherung von links her ( 1- ) bleibt x-1 stets negativ, es ergibt sich also 0- . Die Funktion hat an der Stelle x = 1 eine senkrechte Asymptote. |
|
| 3.Bsp | 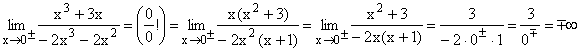 |
 |
Auch hier läßt sich die gemeinsame Nullstelle x = 0 von Zähler und Nenner nur im Zähler vollständig herauskürzen und es ergibt sich der klare Grenzwert -/+¥.. Zu beachten ist hier, dass der Faktor -2 im Nenner die "Vorzeichen " der Null im Nenner umdreht. Die Funktion hat an der Stelle x = 0 eine senkrechte Asymptote. |
| 4.Bsp | 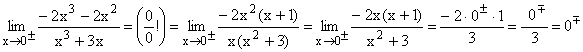 |
| Hier läßt sich die gemeinsame Nullstelle x = 0 von Zähler und Nenner nur im Nenner vollständig herauskürzen und es ergibt sich der klare Grenzwert 0.
Auch hier werden die "Vorzeichen " der Null im Zähler umgedreht. Die Stelle x = 0 ist eine stetig behebbare Definitionslücke von f(x). |