Integralrechnung

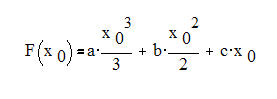
Seite 8 Thema: Einführung in die Integralrechnung

Wie wenden wir diesen Sachverhalt nun an?

Für die allgemeine quadratische Funktion f(x) = ax² + bx +c erhalten wir:

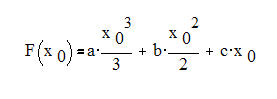
Mit dieser "Flächenformel" können wir alle Parabeln erfassen.

Greifen war eines der Einstiegsbeispiele auf:
-----

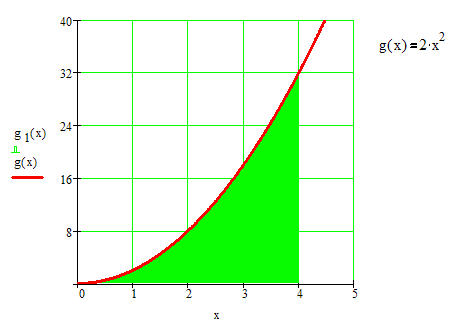
Mit a = 2 und b =0 und c =0 wird f(x) = ax² + bx + c zu f(x)=2x².

--------------

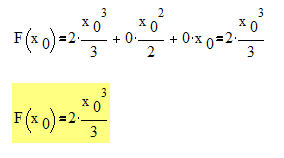
Wir wollen die Fläche unter dem Graphen im Bereich von 0 bis 4 = x₀ berechnen.
Wir setzten den Wert für x₀ in die Flächenformel ein und erhalten:

-------------

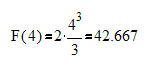
Die Fläche unter dem Graphen beträgt somit A =42,667 FE.

Ein weiteres Beispiel:
----

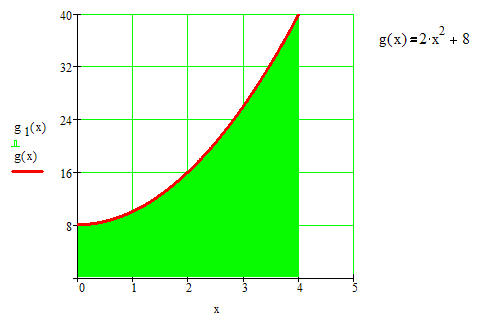
Mit a = 2 und b =0 und c =8 wird f(x) = ax² + bx + c zu f(x)=2x² + 8.

--------------

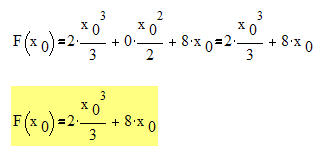
Wir wollen die Fläche unter dem Graphen im Bereich von 0 bis 4 = x₀ berechnen.
Wir setzten den Wert für x₀ in die Flächenformel ein und erhalten:

-------------

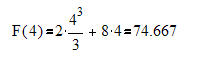
Die Fläche unter dem Graphen beträgt somit A =74,667 FE.

Die Fläche ist genau um 32 FE größer. Wenn Sie das Prinzip der "Integralrechnung" verstanden haben, sollten Sie die Zuwachs erklären können.

Bilden Sie eigene Beispiele, bei denen die Kurvenform immer eine Parabel ist.

Z.B.:

------

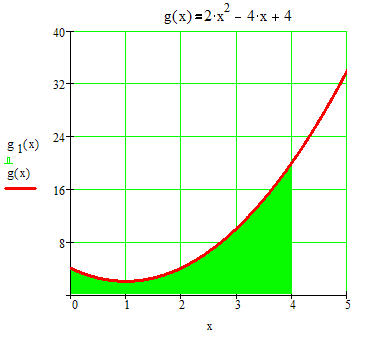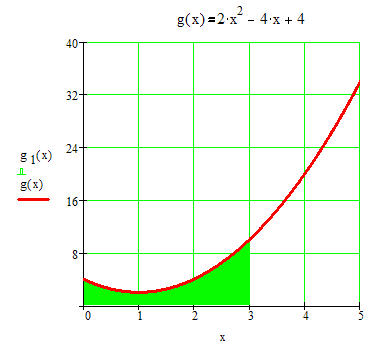
Viel Erfolg!!!!!