 --------------
--------------
Seite 6 Thema: Einführung in die Integralrechnung
Es ist sicherlich leicht zu erahnen. Wir erhöhen die Streifenanzahl und verkleinern damit die Streifenbreite.
----------------- --------------
--------------
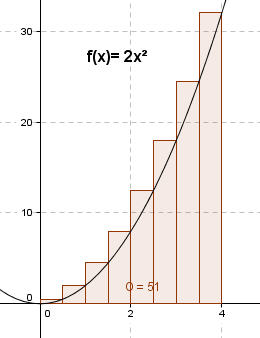
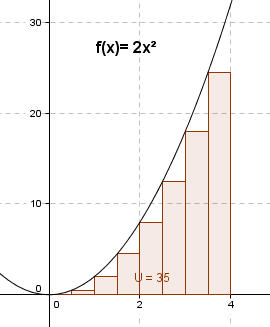
Hier wurden jetzt Streifenbreiten von dx= 0,5 LE gewählt. Die jetzige Abschätzung ergibt: U = 35 FE < A < 51 FE = O
----------------- --------------
--------------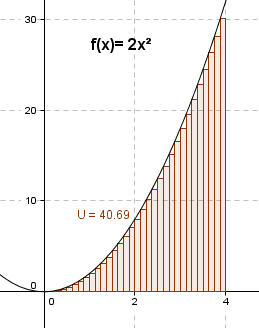
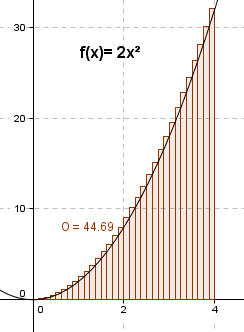
Hier wurden jetzt Streifenbreiten von dx noch kleiner gewählt. Die jetzige Abschätzung ergibt: U = 40,69 FE < A < 44,69 FE = O
Die Anzahl der Streifen können wir beliebig erhöhen. Wie weit sollte es gehen?????
---------------- --------------
--------------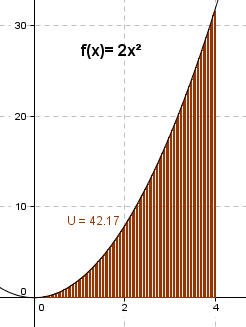
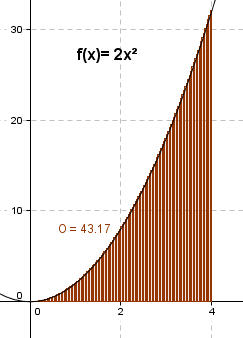
Hier wurden jetzt Streifenbreiten von dx noch kleiner gewählt. Die jetzige Abschätzung ergibt: U = 42,17 FE < A < 43,17 FE = O
Jetzt sollte Sie selbst probieren, wie weit uns die Erhöhung der Streifenanzahl bringt. Applett!!!
Merke: Die Genauigkeit der Methode ist von der Anzahl der Streifen abhängig.
Wie brauchbar unser Vorgehen ist, lässt überprüfen, wenn wir einen bekannten Sachverhalt aufgreifen. Eine lineare Funktion ermöglichte mit der Dreiecksberechnung zur tatsächlichen Fläche.
----------------
-------------- 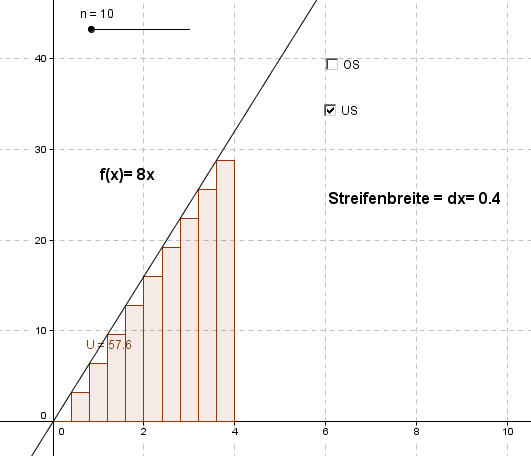
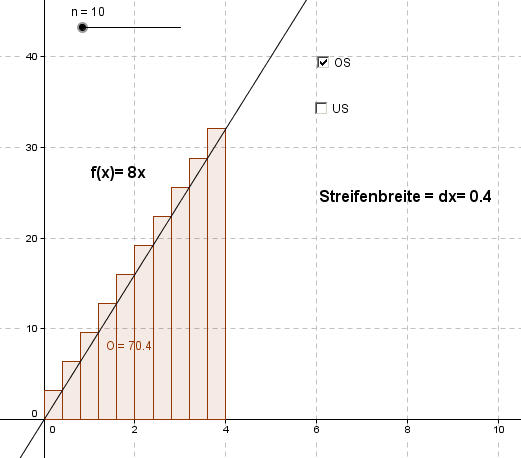
Hier gilt: U = 57,6 FE < A < 70,4 FE = O
Die tatsächliche Fläche liegt bei A= 64 FE. Der Mittelwert aus U und O ergibt auch 64 FE.
-> weiter zur nächsten Seite oder zurück