Seite 5 Thema: Einführung in die Integralrechnung
Die zur erarbeitende Methode greift bereits benutzte Ansätze auf. Wie schon gezeigt, lässt sich die Gesamtfläche auch aus der Summe von Teilflächen berechnen. Zudem haben wir gesehen, dass wir auch näherungsweise einem Ergebnis annähern können.
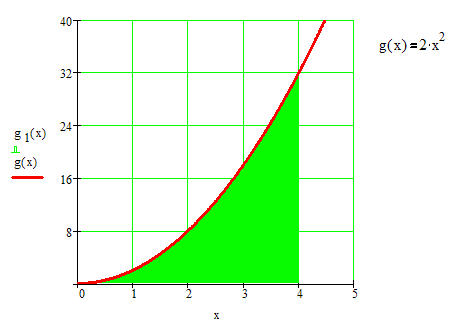
Wir bleiben zunächst bei unserem konkreten Beispiel:
---------- 
Näherungsweise hatten wir bereits festgestellt, dass A< 64 FE sein muss.
-----------------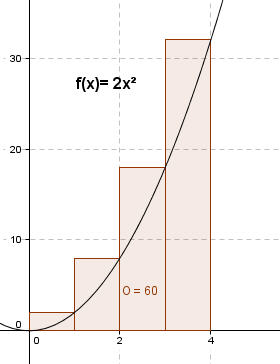
Bei dieser Abschätzung haben wir die Fläche in vier Rechteckstreifen zerlegt, die alle oberhalb der Kurve liegen. Wir nennen die Summe daher auch Obersumme der Rechteckstreifen. Sie können nachrechnen, die Summe diese Flächen ergibt die dort genannte Fläche O= 60FE. Die Streifenbreite ist hier immer dx=1. Bei den Streifenhöhen sollten Sie selbst die Werte finden. Die von uns gesuchte Fläche ist aber immer noch kleiner. Es muss also gelten: A < 60 FE.
Diesen Ansatz können wir jedoch auch mit Rechteckstreifen ausführen, die immer unterhalb der Kurve liegen.
-----------------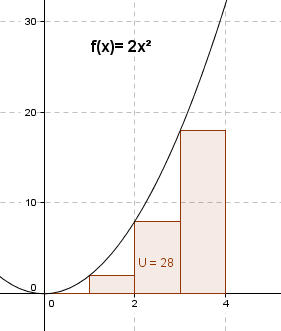
Diese Summe wird folgerichtig mit Untersumme bezeichent. Der Wert liegt offensichtlich bei U= 28 FE. Die von uns gesuchte Fläche ist offensichtlich größer. Wenn wir beide Ansätze kombinieren, dann kommen wir zu folgender Feststellung:
Merke: Die gesuchte Fläche liegt zwischen der Unter- und Obersummen. Kurz: U < A < O
Also: 28 FE < A < 60 FE Bilden wir den Mittelwert der beiden Werte, kommen war auf A ~ 44 FE.
Diese Idee kann verfeinert werden. Wie kann ein besseres Ergebnis erzielt werden? Was würden Sie tun?
-> weiter zur nächsten Seite oder zurück