Seite 4 Thema: Einführung in die Integralrechnung

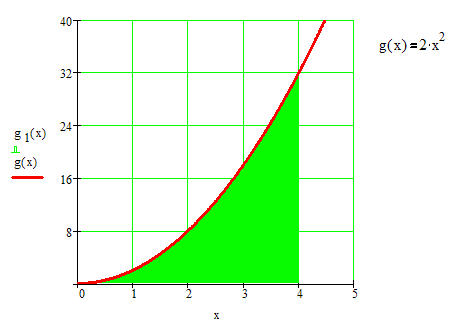
Bei den "einfachen" Beispielen haben wir gesehen, dass die gängigen Formeln zur Berechnung der Flächen ausreichen. Das Ziel der Integralrechnung ist aber auch Flächenberechnungen zu ermöglichen, die mit diesen Formeln nicht gelöst werden können. Bestenfalls können diese Näherungswerte liefern. Betrachten Sie das folgende Beispiel:

----------

Hier könnte als erste Näherung ein Dreieck hinzu gezogen werden. Die zugehörige Fläche des Dreiecks könnten wir berechnen.

----------

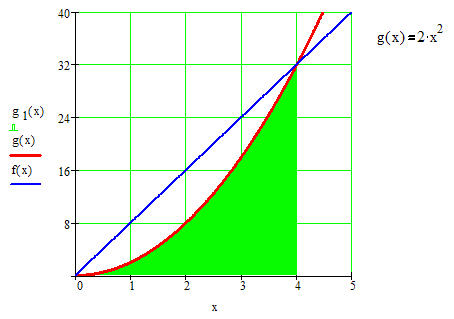
Hier ergibt sich im Intervall [0,4] eine Dreicksfläche von A= 64 FE. (klar???) Die von uns gesuchte Fläche ist offensichtlich kleiner.

Frage: Wie lassen sich Flächen unter nicht lineare Graphen berechnen? (in einem vorgegebenen Intervall, bis zur x-Achse)

Diese Frage gehen wir nun nach!!! Sie ist das eigentliche Problem der Integralrechnung.

-> weiter zur nächsten Seite oder zurück