Seite 3 Lösungen Thema: Einführung in die Integralrechnung

Hier die Lösungshilfen:

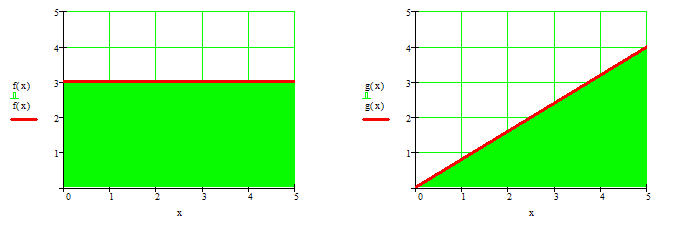
Im ersten Fall ergibt sich für die Fläche unter dem Graphen der Funktion f für das Intervall [0;5] A= 15FE.

Die dargestellte Fläche ist ein Rechteck und mit den erlernten Flächenformel berechnet werden.

Im zweiten Fall ergibt sich für die Fläche unter dem Graphen der Funktion g für das Intervall [0;5] A= 10FE.

In diesem Fall liegt ein Dreieck vor und entsprechend gelöst werden.

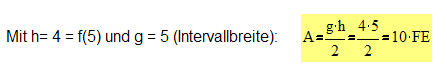
Ansonsten können wir weitere Beispiele aufgreifen:

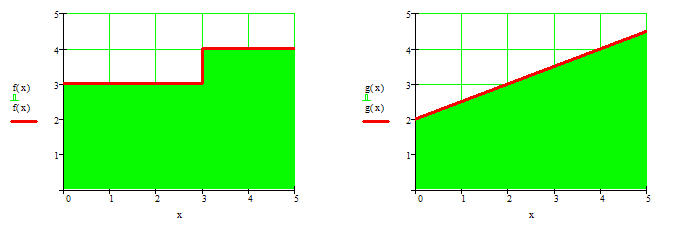
Im dritten Fall ergibt sich für die Fläche unter dem Graphen der Funktion f für das Intervall [0;5] A= 17FE.

Hier wird es schon interessanter. Die dargestellte Fläche kann in zwei Rechtecke zerlegt werden. Die Teilflächen ergeben zusammen den gesuchen Wert und lassen sich wie beim Beispiel 1 erreichnen.

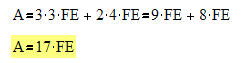
Im vierten Fall ergibt sich für die Fläche unter dem Graphen der Funktion g für das Intervall [0;5] A= 16,25FE.

Auch hier ergibt sich die Gesamtfläche aus zwei Teilflächen, einem Rechteck und einem Dreieck.

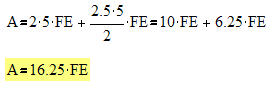
Hier kann aber auch eine weitere Flächenformel das Ergebnis liefern. Als Gesamtfläche liegt hier ein Trapez vor. Prüfen Sie, ob sie das gleiche Ergebnis erhalten?!

Ich hoffe, Sie erinnern sich wieder an diese alten Formeln zur Flächenberechnung. Diese Überlegungen könnten wir fortsetzen, helfen uns aber an dieser Stelle nicht weiter.

-> weiter zur nächsten Seite oder zurück