-----------
Navigation: Seite zurück und Seite vor
Wir behandeln nun alle denkbaren Parabeln. Diese werden allgemein beschrieben durch:
-----------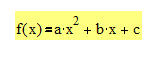
Wir starten nach dem alten Muster:
------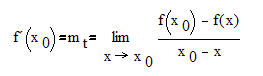
Dann sind:

eingesetzt->
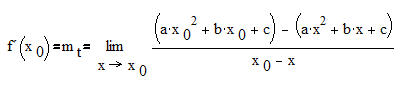
Mit Hilfe der Polynomdivison vereinfache wir:
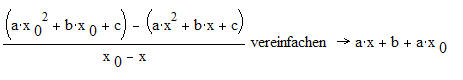
und erhalten nun:
![]()
![]()
Halten wir fest: für die Funktionen der Form f(x) = ax²+bx+c ist die Steigung(sfunktion):
![]()
Wir prüfen unser Ergebnis anhand des Einstiegsbeispiels:
f(x) = 2x² , dann sind a=2 und b = c = 0.
Für x0= 4 ergibt sich: f´(4) = 2•2•4+ 0 = 16 , Tangentensteigung mt = 16 [ok]
Aufgaben:
1.) Es sei f(x)= 2x²-3x-5. Bestimmen Sie f´(x) und ermitteln Sie durch Rechnung die Tangentensteigung der Parabel im Punkt P(3|f(3)).
2.) Es sei f(x)= -3x²+5x. Bestimmen Sie f´(x) und ermitteln Sie durch Rechnung die Tangentensteigung der Parabel im Punkt P(-3|f(-3)).
Aufgaben: Der Rechenweg soll nun teilweise umgekehrt werden.
1.) Es sei f(x)= 2x²-5x-1. Bestimmen Sie f´(x) und ermitteln Sie durch Rechnung die Punkte P(x0|f(x0)) in denen die Tangentensteigung den Wert mt =3 hat.
2.) Es sei f(x)= -3x²+6x-3. Bestimmen Sie f´(x) und ermitteln Sie durch Rechnung die Punkte P(x0|f(x0)) in denen die Tangentensteigung den Wert mt =-3 hat.
Nachdem nun die Funktionen 2. Grades erfasst sind, erhöhen wir den Grad der Funktion.
Haben Sie schon eine Ahnung was sich ergeben wird????? Überlegen Sie und lesen dann weiter.