und damit:
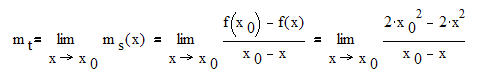
Navigation: Seite zurück und Seite vor
Wir verallgemeinern unser Vorgehen, in dem wir den "festen Punkt P" mit einer Variablen x0 beschreiben. Der zugehörige Funktionswert ist dann f(x0). Wir wollen auch immer noch die Steigung in diesem Punkt bestimmen. Zur Erinnerung: Wir behandeln immer noch die Funktion f(x) = 2x².
Dann ergibt sich:
![]()
und damit:
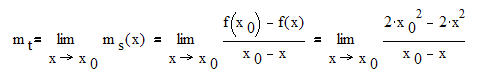
Auch hier sind im letzten Bruch bei x = x0 der Nenner und der Zähler 2x0² - 2x² gleich Null. Es liegt eine Lücke vor. Der Bruch kann vereinfacht werden.
Wir erhalten:
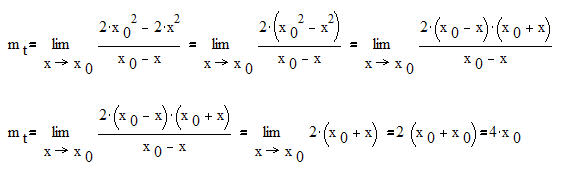
Kurz:
------------![]()
Wie ist dieses Ergebnis zu interpretieren? Was heißt das konkret?
Offensichtlich ist die Steigung für einen beliebigen Kurvenpunkt x0 die Steigung der Tangente immer mt = 4x0.
Also: Für P(4|f(4)) => mt = 4•4=16 , P(2|f(2)) => mt = 4•2= 8, P(-2|f(-2)) => mt = 4•(-2)= - 8 , P(0|f(0)) => mt = 4•0= 0 usw.
Wir können jetzt für die Funktion f(x) = 2x² für jeden beliebigen Punkt P(x0|f(x0)) die zugehörige Steigung berechnen.
Für die Steigung in einem Punkt P(x0|f(x0)) wird zur Vereinfachung geschrieben:
--------------![]()
Wir sprechen von der Ableitung der Funktion und meinen letztlich die Steigung.
Bei der oben vorgenommenen Verallgemeinerung wurde der Punkt P "variabel" gestaltet. Alle Überlegungen beziehen sich immer noch auf die Funktion f(x)=x². Der Graph der Funktion ist eine Parabel.
Im nächsten Schritt wollen wir versuchen nach gleichen Muster alle Parabel zu erfassen.
-----------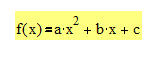
Wenn für die Parabel f(x) = 2x² eine allgemeine Beziehung zur Steigung (Ableitung) besteht, dann ist zu erwarten, dass das auch für die verschobenen Parabeln gilt.