Navigation: Seite zurück und Seite vor
Die Gerade durch die Punkte P und Q hat eine Steigung m, die anhand der Koordinaten der beiden Punkte berechnet werden kann.
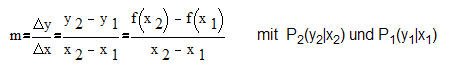
In unserem Beispiel sind z.B. P2(4|32) und Q1(0|0) =P1(0|0) [P1(1|2), P1(2|8)...].
Dann gilt:
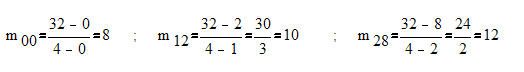
All die Werte sind Steigungen der jeweilgen Sekante.
Für den Fall Q1(4|32) ergibt sich rechnerisch ein Problem. Der Nenner wird zu Null und die Steigung ist auf diesem Wege nicht zu berechnen, die Steigungsformel ist nicht definiert.
Aus diesem Grunde existiert eine solche Sekante nicht und es wird als Darstellungsergebnis "undefiniert" ausgewiesen.
Wenn P und Q "verschmelzen" liegt eine Tangente vor. Die Steigung dieser Tangente ist aber die gesuchte Größe. Wenn wir x1 (= x, ohne Index) veränderlich einsetzen, wird aus der Sekantensteigung eine Sekantensteigungsfunktion m(x). Lassen wir nun den Wert x -> 4 streben, wird aus der Sekantensteigung die gesuchte Tangentensteigung.
------------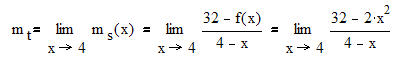
Es ist aber hier eine weitere Besonderheit festzustellen. Es wird an dieser Stelle x=4 nicht nur
der Nenner = 4 - x = 4 -4 =0, sondern auch der Zähler = 32 -2x² = 32 - 2•4² =0.
Es liegt also eine Lücke vor. Der Ausdruck kann somit vereinfacht werden.
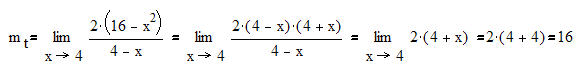
Ergenis: Die Steigung der Tangente hat den Wert mt =16.
1. Auftrag: Prüfen Sie, ob dieses Vorgehen für alle weiteren Punkte Q gilt.
2. Auftrag: Verschieben Sie nun den Punkt P mit xb nach P(5|f(5)) und prüfen Sie den Sachverhalt erneut.
3. Auftrag: Verschieben Sie nun den Punkt P mit xb nach P(-2|8) und prüfen Sie den Sachverhalt erneut.
Im weiteren Verlauf soll der Zusammenhang verallgemeinert werden. Der "feste Punkt" P wird allgemein auf P(x0|f(x0)) gesetzt.