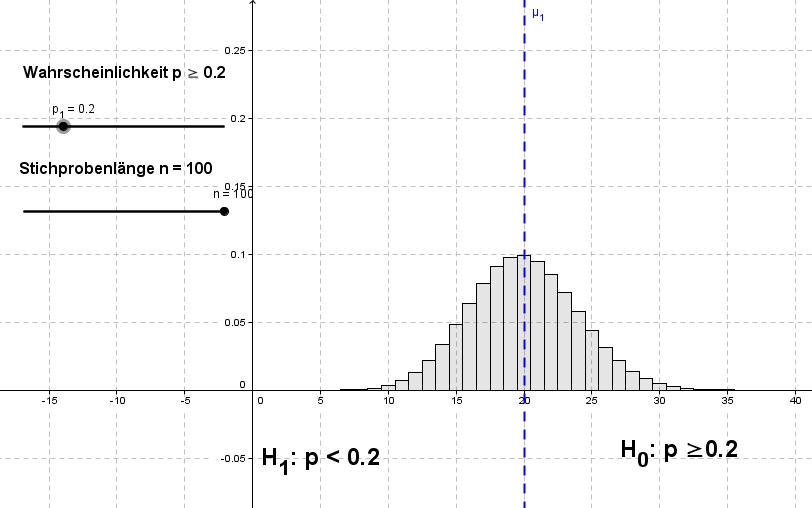
Aufgabenstellung 2:
Bei einem Glücksspiel wird behauptet, dass man mit einer Wahrscheinlichkeit von 20%
gewinnt. Man vermutet, dass die Wahrscheinlichkeit geringer ist.
Also formuliert man die folgenden Hypothesen:
H0: p ≥ 0,2 = 20% ......gegen......... H1: p < 0,2 = 20%
Das Spiel wird 100-mal gespielt, wobei man nur 14-mal gewinnt. Kann man auf einem
Signifikanzniveau von 5% nachweisen, dass die Gewinnwahrscheinlichkeit geringer als 20%
ist?
H0 wird verworfen, wenn k „zu klein“ ist, womit der kritische Bereich auf der linken Seite
liegt. Bei gegebenem Signifikanzniveau (= Wahrscheinlichkeit für den Fehler 1. Art) α muss
in der Tabelle mit den entsprechenden n und p = p0 das größte kO abgelesen werden, für
welches
P(X ≤ kO) ≤ α
gilt. Der kritische Bereich oder Ablehnungsbereich von H0 ist dann K = {0, 1, …, kO}.
Beachte in der Aufgabenstellung: Stichprobenlänge: n= 100 und k=14
Betrachten wir diesen Sachverhalt mit Hilfe des Histogrammes. Der Erwartungswert errechnet sich mit µ=n•p (µ=20).

Wie ist eine untere Grenze kO (nachfolgend kurz k) festzulegen, für welches gilt:
P(X ≤ kO) ≤ α = 0,05
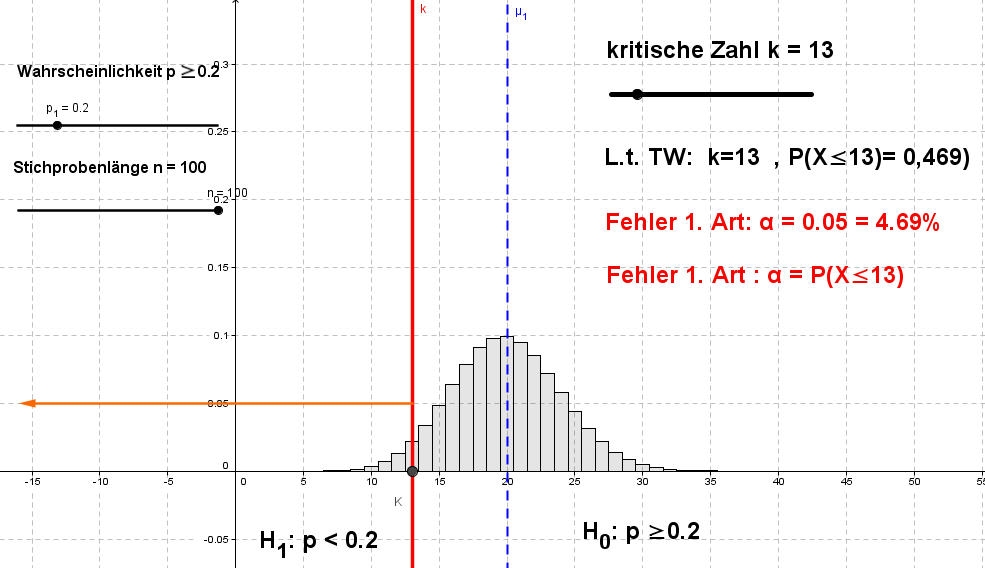
Prüfe mit GeoGebra selbst! Variiere k, bis die geforderte Bedingung erfüllt ist.
GeoGebra(Signifikanztest3) Prüfen Sie zudem mit Hilfe des TW's den ermittelten Wert (siehe FB TW-Tabellen).
Sie werden feststellen, dass bei k =kO= 13 die gewünschte Bedingung erreicht wird.
Der Ablehnungsbereich von H0 ist dann K = {0, 1, ..., 13}.
Da die Nebenwirkung 10-mal im kritischen Bereich liegt, kann H0 verworfen werden und H1 angenommen werden.
Der Fehler 1. Art liegt hier am linken Rand des Histogrammes. Wir sprechen daher von einem linksseitigen Signifikanztest (LST).
Betrachte die abschließende GeoGebra-Version2.
Hat man zusätzlich die Vermutung, dass die Gewinnwahrscheinlichkeit nur 10% beträgt, dann
könnte man auch den Fehler 2. Art, also β, berechnen. Hier kann man im obigen Beispiel
einen Alternativtest formulieren (dieser hat denselben Ablehnungsbereich von H0 wie wenn
die Hypothese „H0: p ≥ 0,2“ gegen „H1: p < 0,2“ getestet wird).
Üben Sie!!!!