Aufgabenstellung 3:
Bei einem Glücksspiel wird behauptet, dass man mit einer Wahrscheinlichkeit von 20%
gewinnt. Dies soll überprüft werden. Dazu wird dieses Spiel 100-mal gespielt und ein Test
mit den Hypothesen H0: p = 0,20 gegen H1 : p ≠ 0,20 auf einen Signifikanzniveau von 5%
durchgeführt. Bei diesen 100 Spielen wurde 11-mal gewonnen. Kann H0 verworfen werden?
Also formuliert man die folgenden Hypothesen:
H0: p = 0,2 = 20% ......gegen......... H1: p ≠ 0,2 = 20%
Wir bestimmen zuerst den kritischen Bereich (bzw. Ablehnungsbereich von H0). Wir müssen
zweiseitig testen (siehe H1) und somit H0 verwerfen, wenn die Anzahl der Gewinne „zu klein“
oder „zu groß“ ist. Somit hat der Ablehnungsbereich von H0 folgende Gestalt:
K = {0, 1, …, kO} U {ku , …, 100}.
Nun muss in der kumulierten Tabelle der Binomialverteilung für n = 100 und p = 0,2 das
größtekO und das kleinste ku abgelesen werden, für welche die Gleichungen
(1) P(X ≤ kO) ≤ α/2 = 0,025 und
(2) P(X ≥ ku) ≤ α/2 = 0,025
gelten.
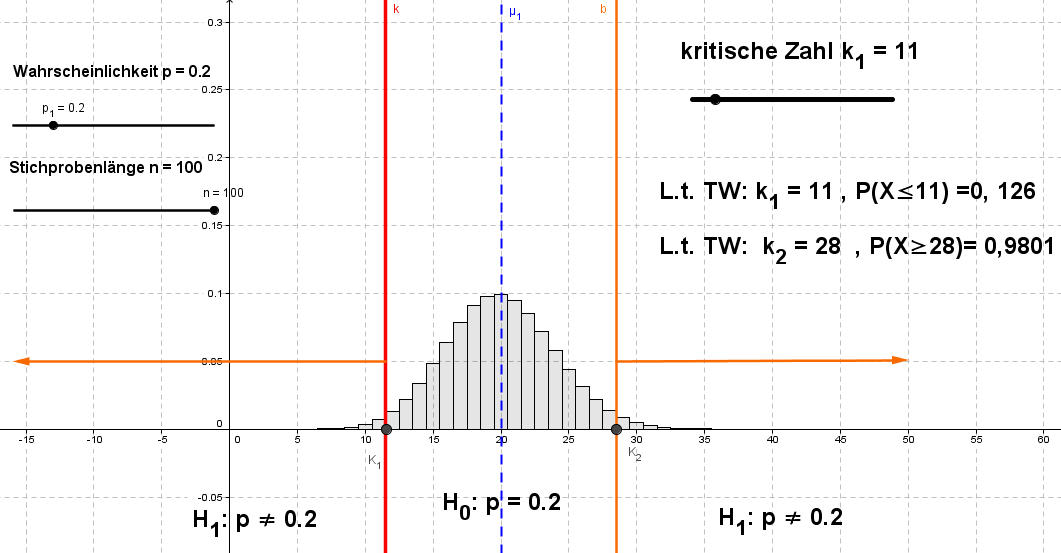
Betrachten wir diesen Sachverhalt mit Hilfe des Histogrammes. Der Erwartungswert errechnet sich mit µ=n•p (µ=20).

Die beiden Bereiche der Ablehnung sind symmetrisch angeordnet.
(1) P(X ≤ kO) ≤ α/2 = 0,025...... und ......(2) P(X ≥ ku) ≤ α/2 = 0,025
Prüfe mit GeoGebra selbst! Variiere k, bis die geforderte Bedingung erfüllt ist.
GeoGebra(Signifikanztest4) Prüfen Sie zudem mit Hilfe des TW's den ermittelten Wert (siehe FB TW-Tabellen).
Damit ist kO = 11 und ku– 1 = 28 bzw. ku = 29: K = {0, 1, …, 11} U {29, …, 100} (Ablehnungsbereich von H0.
Im Beispiel wurde 11-mal gewonnen. Da 11 in K liegt, kann man mit einer Irrtumswahrscheinlichkeit von α = 5% die Nullhypothese verwerfen.
Der Fehler 1. Art liegt hier am linken und rechten Rand des Histogrammes. Wir sprechen daher von einem beidseitigen oder auch zweiseitiger Signifikanztest (BST).
Weitere Übungen bei Binkmann: Übungen1 und Übungen2.
Zudem ist es ratsam alte Abiturprüfungen zu diesem Thema zusammeln.
Weiter geht es mit den Hypotesentests mittels Umgebungsgrößen.
ENDE