|
Begriff / Verfahren
|
Beschreibung
|
| Bestimmen der Käuferzahlen zu Beginn des Zeitraumes |
Die Anzahl der Käufer einer
jeden Illustrierten berechnet sich aus der gesamten Käuferzahl
( 60.000 ) nach den Regeln der Prozentrechnung:
40% kaufen die Illustrierte
A: Rechnung :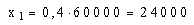
20% kaufen die Illustrierte
B: Rechnung :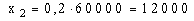
40% kaufen die Illustrierte
C: Rechnung :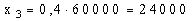 
|
|
Darstellung der Käuferzahlen als Vektor
Allgemeine Definition: Vektor
|
Die Ergebnisse für die
drei Illustrierten lassen sich in dem folgenden Zahlenschema zusammenhängend
darstellen: 
= 
(siehe auch: Definition
1)
Wir haben diese
Darstellung Käufervektor genannt und ihn mit  bezeichnet.
|
| Aufstellen der Verteilungstabelle |
Die Angaben über das Käuferverhalten
lassen sich übersichtlich in einer Tabelle darstellen. Es empfiehlt
sich, die Tabelle so anzulegen, dass in den Zeilen die Werte stehen,
die eine Illustrierte von allen anderen erhält. (
Begründung siehe: Multiplikation einer Matrix mit
einem Vektor)
| |
A: (gibt ab an) |
B: (gibt ab an) |
C: (gibt ab an) |
| A:( erhält von) |
0,8
|
0,3
|
0,2
|
| B:( erhält von) |
0,1
|
0,5
|
0,1
|
| C :(erhält von) |
0,1
|
0,2
|
0,7
|
|
|
Definition der Verteilungsmatrix
Allgemeine Definition: Matrix
|
Das Zahlenschema der Tabelle
nennen wir Matrix. V
= 
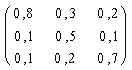
Die Matrix hat in diesem Fall
3 Zeilen (waagerecht) und 3 Spalten (senkrecht)t.
Dabei wird auf die Darstellung
der Bedeutung der Zeilen und Spalten verzichtet
|
|
Multiplikation einer Matrix mit einem Vektor
Allgemeine Definition:
Matrix "mal" Vektor
|
Wenn wir mit Hilfe der Tabelle
die Käufer nach der 1..Woche berechnen haben wir folgende Rechnung
auszuführen:
|
|
von A:
|
von B:
|
von C:
|
Käufer
|
| A:( erhält von) |
0,8*24000+
|
0,3*12000+
|
0,2*24000
=
|
27600
|
| B:( erhält von) |
0,1*24000+
|
0,5*12000+
|
0,1*24000
=
|
10800
|
| C :(erhält von) |
0,1*24000+
|
0,2*12000+
|
0,7*24000
=
|
21600
|
Gehen wir von der Tabelle zur
Matrix über, so können wir diese Rechnung auch vereinfacht
in folgender Form schreiben, wenn wir eine geeignete Multiplikation
definieren:
= V  =
*
= 
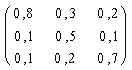Das Zeichen
"
" bedeutet die Matrizenmultiplikation für
Vektoren, die wie folgt ausgeführt wird:
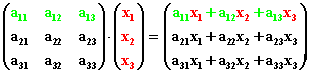
Nur weil in
den Zeilen unserer Matrix ( und natürlich auch der Tabelle
)die Werte stehen, die eine Illustrierte von allen anderen erhält,
können wir die Berechnungen mit Hilfe der Matrizenmultiplikation
durchführen.
|
| Berechnen der Käufervektoren für die einzelnen
Wochen |
Die Käufervektoren der
folgenden Wochen berechnen sich über die Matrizenmultiplikation
der Matrix V mit dem Käufervektor der Vorwoche gemäss
der Gleichung:
= V  ,
dabei ist i der Index für die jeweilge Woche
|
