| Station 11 | Matrixprodukt und Abbildungen |  |
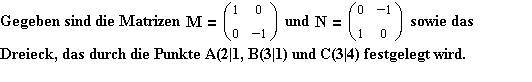
Aufgabe
1:
a. Berechnen Sie 
=
M
, 
=
M
,
= M
und und
zeichnen Sie
das gegebene Dreieck und das durch die Ortsvektoren ,
und
festgelegte Dreieck in ein Koordinatensystem ein.
b. Berechnen Sie nun die
Matrix-Vektor-Produkte N ,
Nund
N und
zeichnen Sie dieses Dreieck ebenfalls in das Koordinatensystem ein.
Was für eine Abbildung ist insgesamt entstanden?
Aufgabe
2:
Es
gelten die Definitionen wie bei Aufgabe 1. Berechnen und zeichnen Sie
= N
,
= N
,
= N
sowie die Matrix-Vektor-Produkte M,
M
und
M.
Was für eine Abbildung entsteht nun?
Aufgabe 1 und Aufgabe 2 zeigen, dass man beim Matrixprodukt nicht die Faktoren vertauschen darf, wie man es von den reellen Zahlen gewohnt ist.
Aufgabe 3:
Beweisen Sie allgemein, dass die Produktmatrix der Abbildung entspricht, die durch die verkettete Abbildung N°M festgelegt wird.
| zurück |
