| Station 11 | Matrixprodukt und Abbildungen |
|
Lösung zu Aufgabe 1:
Die Matrizen M und N sind aus der Station "Station elementare Abbildungen in der Ebene" schon bekannt:
M (dort:M1) ist eine Spiegelung an der x-Achse, N (dort M4) ist eine Drehung im Koordinatenursprung um 90°.
Führt man die Abbildungen hintereinander aus (erst M und dann N), so liefert die Matrix-Vektor-Multiplikation:
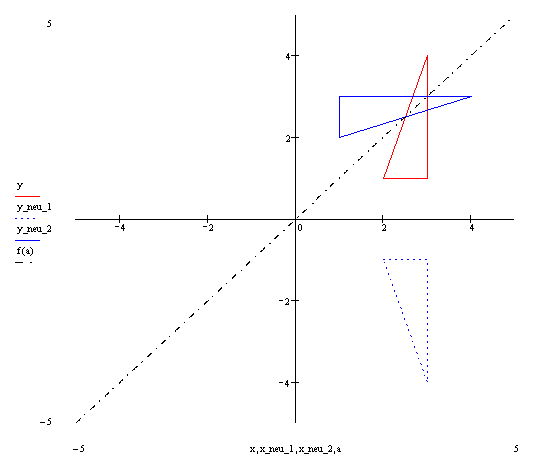
Fazit: Das gegebene Dreieck wird insgesamt an der Geraden y = x gespiegelt.
Bei dieser Abbildung, bei der zuerst M und dann N ausgeführt wurde, erhält man die Verkettung N°M. Für die Berechnung der Eckpunkte des Dreiecks, das durch die Verkettung N°M entsteht, gilt:
Der verketteten Abbildung N°M entspricht die Abbildung, die durch die Produktmatrix P = N*M gegeben wird, wie die entsprechenden Matrix-Vektor-Multiplikationen zeigen:
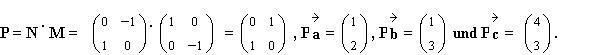
Dabei ist zu beachten, dass der zweite Faktor M der zuerst ausgeführten Abbildung entspricht.
| zurück |
