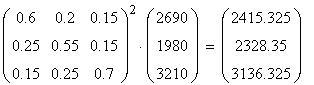| Station 15 | Markoff-Kette |
Die
Geschäftsführerin des Modegeschäfts Shorthouse gibt
eine Untersuchung des Einkaufsverhalten der Kunden in der Innenstadt in
Auftrag.
Eine Umfrage ergibt folgendes Ergebnis:
60% der Monatskunden von
Shorthouse kaufen auch im folgenden Monat dort, während 25%
zu Morgan´s und 15% zu Jeansfit abwandern.
Andererseits bleiben 55%
der Kunden von Morgan´s diesem Geschäft auch im folgenden
Monat treu, während 20% zu Shorthouse und 25% zu Jeansfit
wechseln.
Jeansfit kann dagegen 70% seiner Kunden an sich binden, verliert
aber pro Monat jeweils 15% seiner Kunden an Shorthouse und an Morgan´s.
Im untersuchten Monat kauften
2690 Personen bei Shorthouse, 1980 bei Morgan´s
und 3210 bei Jeansfit.
Die Geschäftsführerin
interessiert die zu erwartende Kundenverteilung in den nächsten sechs
Monaten, um über mögliche Werbemaßnahmen entscheiden zu
können. Dabei wird davon ausgegangen, dass die Zahl der Kunden in
der Innenstadt insgesamt konstant bleibt.

Solche zufallsartigen Prozesse
können mit der Matrizenrechnung relativ einfach untersucht werden.
Dazu bildet man zunächst die Übergangsmatrix,
die in den Zeilen die Übergangswahrscheinlichkeiten
enthält. Die Spaltensummen einer Übergangsmatrix ergeben stets
1. Da zudem alle Matrixelemente positiv oder null sind, spricht man von
einer stochastischen Matrix.
|
Wanderung von / zu
|
Shorthouse
|
Morgan´s
|
Jeansfit
|
|
Shorthouse
|
0,6
|
0,2
|
0,15
|
|
Morgan´s
|
0,25
|
0,55
|
0,15
|
|
Jeansfit
|
0,15
|
0,25
|
0,7
|
Diese Matrix beschreibt
einen Zufallsprozess, bei dem ein Zustand (oder Ereignis) nur vom unmittelbaren
Vorgänger beeinflusst wird und selbst nur Einfluss auf den unmittelbar
folgenden Zustand hat. Einen solchen stochastischen Prozess nennt man
nach dem russischen Mathematiker
Andrei Andrejewitsch Markoff (1856-1922)
Markoff-Kette.
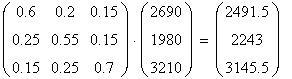
Mulitpliziert man die Übergangsmatrix nun mit diesem Ergebnisvektor,
erhält man die Verteilung nach zwei Monaten usw.:

Aufgabe:
a) Berechnen Sie die Kundenverteilung nach 4 und nach 6 Monaten.
b) Eine mögliche Werbekampagne für Shorthouse würde
70% der Kunden an das Geschäft binden, nur noch 20% würden zu
Morgan´s und nur noch 10% zu Jeansfit wechseln.
c) Untersuchen Sie, welchen Effekt die in b) beschriebene Werbemaßnahme
nach zwei bzw. nach drei Jahren hätte. Was fällt Ihnen auf?
| zurück |