Eine Variation ist eine Kombination, die aber über die Kombination hinaus noch die möglichen Reihenfolgen als weitere Möglichkeiten umfasst.zentrale Fragestellung:Bei Variationen geht es grundsätzlich darum, einige Elemente aus der Ausgangsmenge auszuwählen und zusätzlich in eine bestimmte Reihenfolge zu bringen.
Wieviele Möglichkeiten gibt es,Variation ohne Wiederholung
- einige Elemente der Ausgangsmenge auszuwählen
- und in einer Reihenfolge anzuordnen ?
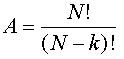
Voraussetzungenzentrale Frage
- Alle (N) Elemente der Ausgangsmenge unterscheiden sich voneinander.
- Es werden einige (k) Elemente ausgewählt.
- Ein Element kann nicht mehrmals ausgewählt werden.
Wieviele Möglichkeiten gibt es, k Elemente auszuwählen und in eine Reihenfolge zu bringen?einfaches BeispielAus 3 unterschiedlichen Elementen sollen 2 ausgewählt werden und in die möglichen Reihenfolgen angeordnet werden. Ein bestimmtes Element kann nur einmal ausgewählt werden.prototypisches Beispiel
Zunächst stellt sich die Frage, wieviele mögliche unterschiedliche 2 Elemente ausgewählt werden können. Liegen alle möglichen 2 Elementekombinationen vor, muß noch die Anzahl der möglichen Reihenfolgen aus den Kombinationen ermittelt werden.mögliche Auswahlen Reihenfolge relevant Ausgangsmenge (Kombinationen) alle möglichen Anordnungen1 2 3 12 13 23 12 21 13 31 23 32N=3 k=2A = N!/(N-k)! A = 3!/(3-2)! = 6Es gibt 6 Möglichkeiten, 2 Elemente ohne Wiederholung aus 3 Elementen auszuwählen und in eine Reihenfolge zu bringen.Gold, Silber, BronzeVertiefung:
8 Läufer stehen im Finale der Olympischen Spiele.
Wieviele Möglichkeiten gibt es, daß die 8 Läufer Gold, Silber und Bronze unter sich ausmachen.
- Es kann nur einmal Gold, einmal Silber und einmal Bronze vergeben werden (= ohne Wiederholung).
- Es kommt auf die Reihenfolge an. d.h. z.B. Wenn wir wissen, daß Läufer a,b,c die Medaillen unter sich ausgemacht haben, dann gibt es noch mehrere Möglichkeiten, wer jeweils welches Metall erhalten haben könnte (Reihenfolge relevant).
N = Anzahl der Finalisten = 8 k = Medaillen = 3A = N!/(N-k)! A = 8!/(8-3)! = 40320/120 = 336Es gibt 336 Möglichkeiten, unter 8 Finalisten Gold, Silber und Bronze zu verteilen.Es gibt N!/((N-k)!*k!) = 40320/(120*6) = 56 unterschiedliche Kombinationen (Reihenfolge irrelevant) für die ersten 3 Läufer, die durchs Ziel kommen. Für jede dieser möglichen Kombinationen aus 3 Läufern gibt es aber 3! mögliche Reihenfolgen:Exkurs
56 * 6 = 336 mögliche MedaillenverteilungenDie Permutation ohne Wiederholung ist ein Spezialfall der Variation ohne Wiederholung. Werden bei der Variation ohne Wiederholung alle Elemente ausgewählt, so ergeben die Formeln für beide Varianten das gleiche Ergebnis.
N! = N! / (N-N)! , weil 0!=1
Voraussetzungen
zentrale Frage
- Alle (N) Elemente der Ausgangsmenge unterscheiden sich voneinander.
- Es werden einige (k) Elemente ausgewählt.
- Ein Element kann mehrmals ausgewählt werden.
Wieviele mögliche Reihenfolgen unter den möglichen auswählbaren Elementen gibt es?einfaches Beispiel:Aus 3 unterschiedlichen Elementen sollen 2 Elemente ausgewählt und angeordnet werden.Prototypisches Beispiel
- Es stehen 3 Elemente jederzeit zur Verfügung. d.h. zieht man ein Element, so verschwindet es nicht aus der Ausgangsmenge, sondern bleibt erhalten. (= mit Wiederholung)
- Zunächst stellt sich die Frage, wieviele mögliche 2 Elemente ausgewählt werden können. Liegen alle möglichen Zweierkombinationen vor, muß noch die Anzahl der möglichen Reihenfolgen aus den Kombinationen ermittelt werden. (=Reihenfolge relevant)
mögliche Auswahlen Reihenfolge relevant Ausgangsmenge (Kombinationen) alle möglichen Anordnungen1 2 3 11 12 13 22 23 33 11 12 13 22 23 33 21 31 32N=3 k=2 A = Nk = 32 = 9Es gibt 9 Möglichkeiten, mit Wiederholung aus 3 Elementen 2 Elemente auszuwählen und in eine bestimmte Reihenfolge zu bringen.Hinweis 1: Im Gegensatz zur Variation ohne Wiederholung können hier bestimmte Elemente mehrmals ausgewählt werden (22,33). Die Kombinationen 22 bzw. 33 können aber nur eine Reihenfolge haben.
Hinweis 2. k kann größer als N sein, weil jedes Element aus k mehrfach gezogen werden kann. [z.B. 9 Elemente aus der Ausgangsmenge: etwa 111122223]
Zahlenschloss
Ein Zahlenschloss bestehe aus 5 Vorrichtungen, welche jeweils eine Zifferneinstellung verlangen. Wieviele Möglichkeiten gibt es ?wichtig
- Bei jeder Zifferneinstellung können die Zahlen 0 bis 9 gewählt werden (N=10). Bestimmte Ziffern können mehrfach vorkommen (=mit Wiederholung)
- Die Reihenfolge ist entscheidend (01557 ist ungleich 75510)
N = 10 mögliche Ziffern (0 bis 9) k = 5 Zifferneinstellungen A = Nk = 105 = 100000Es gibt 100 000 mögliche Ziffernanordnungen für ein Zahlenschloss mit 5 einzustellenden Ziffern.Merke! Die richtige Zahlenkombination (=Menge der zutreffenden Zahlen) genügt nicht, um ein Schloss zu öffnen, man braucht die richtige Zahlenvariation (=Reihenfolge der Zahlen)