Kombinationen (Reihenfolge irrelevant)
Bei Kombinationen geht es grundsätzlich darum, einige Elemente aus der Ausgangsmenge lediglich auszuwählen.zentrale Fragestellung
Wieviele unterschiedliche Möglichkeiten gibt es, eine bestimmte Anzahl von Elementen der Ausgangsmenge auszuwählen ?Kombination ohne Wiederholung
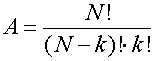
Voraussetzungenzentrale Frage: Wieviele mögliche unterschiedliche Elementenzusammensetzungen (=Kombinationen) gibt es ?
- Alle (N) Elemente der Ausgangsmenge unterscheiden sich voneinander.
- Es werden einige (k) Elemente ausgewählt.
- Ein Element kann nicht mehrmals ausgewählt werden.
Einfaches Beispiel
Es stehen 4 unterschiedliche Elemente zur Verfügung. Zieht man ein Element, so verschwindet es aus der Ausgangsmenge und kann nicht noch einmal gezogen werden. Es sollen 2 Elemente ausgewählt werden. Wieviele mögliche unterschiedliche Kombinationen gibt es ?Es gibt 6 Möglichkeiten ohne Wiederholung 2 Elemente aus 4 Elementen auszuwählen.mögliche unterschiedliche mögliche Reihenfolgen Ausgangsmenge Auswahlen (Kombinationen) irrelevant1 2 3 4 12 13 14 23 24 34N=4 k=2A = N!/((N-k)!*k!) A = 4!/((4-2)!*2!) = 6Prototypisches Beispiel
Ziehung der Lottozahlen
Aus 49 nummerierten Kugeln werden nacheinander 6 Kugeln gezogen.
Wieviele mögliche 6 Zahlen können ausgewählt werden ?Wichtig:
Es werden einige Kugeln aus mehreren Kugeln gezogen.
Eine gezogene Kugel kann nicht noch einmal ausgewählt werden.
Es spielt keine Rolle, in welcher Reihenfolge die Kugeln gezogen werden.N=49; k=6;
A = N!/((N-k)!*k!)
A= 49!/((49-6)!*6!) = 13983816Es gibt ca. 14 Millionen Möglichkeiten, 6 Zahlen im Lotto anzukreuzen.
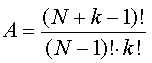
Voraussetzungenzentrale Frage
- Alle Elemente der Ausgangsmenge unterscheiden sich voneinander.
- Es werden einige Elemente ausgewählt.
- Ein Element kann mehrmals ausgewählt werden.
Wieviele mögliche unterschiedliche ausgewählte Elementenzusammensetzungen (=Kombinationen) gibt es ?einfaches BeispielEs stehen 4 unterschiedliche Elemente jederzeit zur Verfügung. D.h.: Zieht man ein Element, so verschwindet es nicht aus der Ausgangsmenge, sondern bleibt erhalten. Man kann sich z.B. eine Kugelspendermaschine vorstellen, die 4 verschieden farbige Kugeln zum Entnehmen anbietet. Zieht man die rote Kugel, dann kommt von unten die nächste rote Kugel nach.Es sollen 2 Elemente aus der Ausgangsmenge ausgewählt werden. Wieviele mögliche unterschiedliche Elementenzusammensetzungen gibt es ?
mögliche Auswahlen Reihenfolge Ausgangsmenge (Kombinationen) irrelevant1 2 3 4 11 12 13 14 22 23 24 33 34 44N=4 k=2A = (N+k-1)!/((N-1)!*k!) A = (4+2-1)!/( 3! *2!) = 120/12 = 10Es gibt 10 Möglichkeiten mit Wiederholung aus 4 Elementen 2 Elemente auszuwählen.Prototypisches Beispiel
Wiederholung erkennt man hier an den Elementenzusammensetzungen (11,22,33,44). Dasselbe Element kann eben hier genau 2 mal gezogen werden, weil k=2.3 Päckchen Zigaretten aus dem Zigarettenautomat
Aus einem prall gefüllten Zigarettenautomat mit 15 Fächern kann man 15 verschiedene Zigarettensorten auswählen. Sie erhalten den Auftrag, 3 Päckchen Zigaretten zu besorgen, wobei es egal ist, um was es sich dabei handelt, da es dem Raucher nur um Nikotin geht.
Wieviele mögliche Zusammensetzungen von unterschiedlichen 3 Zigarettenpäckchen gibt es.
Wichtig:Für jede Ziehung stehen alle Zigarettensorten zur Verfügung. D.h. sie können mehrmals dieselbe Marke ziehen (mit Wiederholung). Es spielt keine Rolle, in welcher Reihenfolge die Zigarettenpäckchen gezogen werden (Reihenfolge irrelevant). N = 15 Zigarettensorten k = 3 ZigarettenpäckchenA = ( N+k-1)!/(( N-1)!*k!) A = (15+3-1)!/((15-1)!*3!) A = 680 mögliche unterschiedliche 3 Zigarettenpäckchenkombinationen