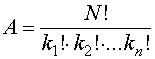Bei Permutationen geht es grundsätzlich darum, alle Elemente der Ausgangsmenge in eine bestimmte Reihenfolge zu bringen:

Wieviele Möglichkeiten gibt es, alle Elemente der Ausgangsmenge anzuordnen ?

Voraussetzungen

1. Alle (N) Elemente der Ausgangsmenge unterscheiden sich voneinander.
2. Es müssen alle (N) Elemente ausgewählt werden.
3. Ein Element kann nicht mehrmals ausgewählt werden.

Zentrale Frage: Wieviele mögliche unterschiedliche Reihenfolgen gibt es ?

einfaches Beispiel

Ausgangsmenge   Auswahl           alle möglichen
N = 3           (Kombination)     Anordnungen
                
1 2 3           1 2 3             123  
                                  132
                                  213
                                  231
                                  312
                                  321

Anzahl der Möglichkeiten A = N!  = 3! = 1*2*3 = 6

Es gibt 6 Möglichkeiten, 3 Elemente (Objekte) in eine unterschiedliche Reihenfolge zu bringen.

Prototypisches Beispiel
Zielankunft beim 100 Meter - Endlauf

8 Läufer beim 100-Meter-Endlauf kommen in einer bestimmten Reihenfolge durch das Ziel.
Auf der Anzeigetafel werden die Läufer nacheinander entsprechend Ihrem Rangplatz aufgelistet. Die tatsächliche Platzierung der Läufer entspricht einer möglichen Anordnung.

Wieviele mögliche Reihenfolgen hat es vor der Zielankunft gegeben?

N=8;  N!= 1*2*3*4*5*6*7*8 =   40320

Es gibt 40320 mögliche unterschiedliche Zieleinläufe beim 100 Meter-Finale.

Voraussetzungen

1. Mindestens 2 Elemente der Ausgangsmenge sind identisch, d.h. die Elemente der Ausgangsmenge unterscheiden sich nicht alle voneinander.
2. Es müssen alle (N) Elemente ausgewählt werden.
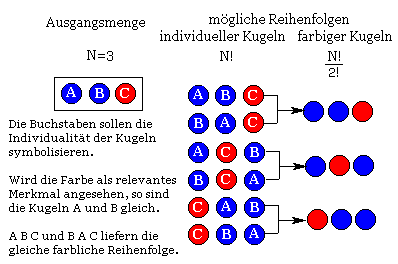
3. Ein Individualelement kann nicht mehrmals ausgewählt werden, ein Element mit gleicher Eigenschaft hingegen schon.  Liegen z.b. 2 rote Kugeln in der Ausgangsmenge, so muss jede der beiden roten Kugeln ausgewählt werden (Wiederholung), eine dritte rote Kugel kann aber nicht ausgewählt werden.

 
zentrale Frage: Wieviele mögliche Reihenfolgen gibt es ?

      A = Anzahl der Möglichkeiten
      N = Anzahl aller Elemente
 k1..kn = Anzahl der Elemente mit gleichen Eigenschaften
      A = N!/(k1!*..*kn!)

einfaches Beispiel

Ausgangsmenge   Auswahl          alle möglichen Anordnungen
                (Kombination)

1 1 2           1 1 2            112    121    211

     N=3             k1=2,k2=1

k1 = Anzahl der Elemente mit der Eigenschaft 1 = 2
k2 = Anzahl der Elemente mit der Eigenschaft 2 = 1

 A = N!/(k1! * k2!)  
 A = 3!/( 1! * 2! ) = 3

Exkurs: Wenn ein Element nur einmal vorkommt (k_x=1), so kann es weggelassen werden, weil 1! = 1. Bei der Permutation ohne Wiederholung sind alle k₁ bis k_n = 1. Der Nenner ergibt sich zu 1 und es verbleibt N!.

Vertiefung


Prototypisches Beispiel
Mögliche Buchstabenanordnungen beim Wort ANAGRAMM
 

Wieviele unterschiedliche Möglichkeiten gibt es, alle Buchstaben des Wortes ANAGRAMM
in einer unterschiedlichen Reihenfolge anzuordnen. In diesem Wort kommen bestimmte Buchstaben mehrfach vor.

Anzahl aller Buchstaben: N=8
Häufigkeit einzelner Buchstaben:

k1 = A = 3
k2 = G = 1
k3 = N = 1
k4 = M = 2
k5 = R = 1

A =  8!/(3!*1!*1!*2!*1!) = 8!/(3!*2!) = 40320/12 = 3360

Es gibt 3360 unterschiedliche (8 Buchstaben umfassende) Wörter, die unter der Verwendung aller Buchstaben des Wortes ANAGRAMM gebildet werden können.


Hinweis: Die Permutation mit Wiederholung ist der einzige, hier betrachtete Fall, bei dem in der Ausgangsmenge gleiche Elemente vorkommen (z.B. 2 rote Kugeln).