Übungsaufgaben: Lösung zu Aufgabe 12b
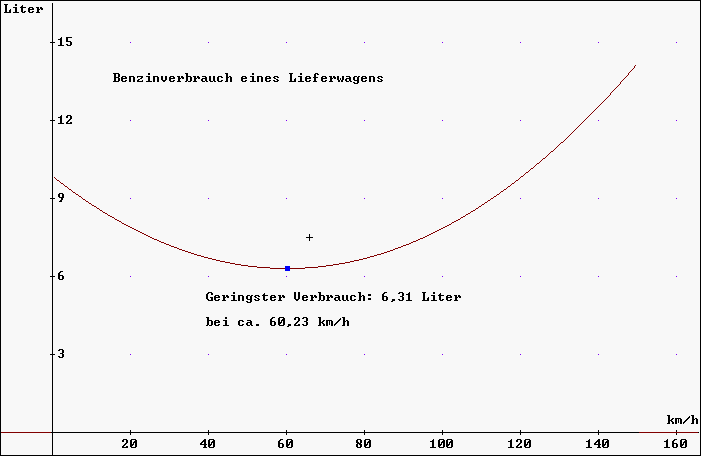
Berechnung der Geschwindigkeit für den geringsten Benzinverbrauch:
DERIVE liefert für die Verbrauchsfunktion V:

Man bildet nun die erste Ableitung V'(x) und löst mit DERIVE das Problem: V'(x) = 0.

Ergebnis: x » 60,23 . Das heißt: Bei einer Geschwindigkeit von ca. 60,23 km/h hat der Lieferwagen den geringsten Benzinverbrauch.

Die Maßzahl für den geringsten Verbrauch ergibt sich dann aus: V(60.23) » 6,31 (Liter).
Für den Verbrauch bei 150 km/h Geschwindigkeit ergibt sich mittels DERIVE : V(150) » 14,2 (Liter).
                             
Die Berechnungen hierzu finden Sie wieder im DERIVE-File  Übungsaufgabe 12.mth  im Anhang!