Düngung eines Erdbeerfeldes - Ertragskurve: Lösung zu Aufgabe 2.3

Der Ansatz für eine ganzrationale Funktion f   4. Grades lautet:

f(x) = a·x⁴ + b·x³ + c·x² + d·x + e    mit a, b, c, d, e ÎIR.
f '(x) = 4·a·x³ + 3·b·x² + 2·c·x + d

Aufgrund des Aufgabentextes ergeben sich folgende 5 Gleichungen:

(1) f(0) = 4 Û e= 4
(2) f(1) = 12 Û a·1⁴ + b·1³ + c·1² + d·1 + 4 = 12 Û a + b + c + 4 = 12
(3) f '(1) = 0 Û 4·a·1³ + 3·b·1² + 2·c·1 + d= 0 Û 4·a + 3·b + 2·c = 0
(4) f '(0) = 0 Û d= 0
(5) f(2) = 0 Û a·2⁴ + b·2³ + c·2² + d·2 + 4 = 0 Û 16·a + 8·b + 4·c + 4 = 0

Mittels DERIVE löst man nun das Gleichungssystem (vgl. den DERIVE-File
Erdbeerdüngung.mth) und als Funktionsgleichung für die Ertragskurve erhält man:
(Dazu verwendet man entweder den Befehl SOlVE([f(0)=4,f(1)=12,...],[a,b,c,d,e]) oder man löst das oben stehende Gleichungssystem mit dem Befehl Solve > System.)

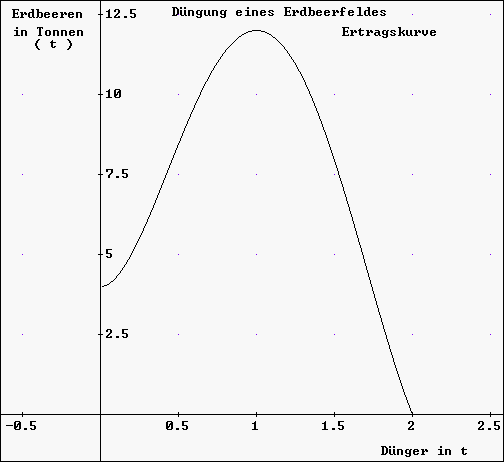
Mittels der CHI-Funktion [CHI(0,x,2)*F(x) ] lässt sich dann die Ertragskurve zeichnen: