ST- und FT-Muskelfaser: Spannung in Abhängigkeit von der Zeit:
Lösung zu Aufgabe 1.2

f(x) = a·x⁷ + b·x⁶ + c·x⁵ + d·x⁴ + e·x³ + g·x² + h·x + i
f '(x) = 7·a·x⁶ + 6·b·x⁵ + 5·c·x⁴ + 4·d·x³ + 3·e·x² + 2·g·x + h

Die 8 Bedingungen (Gleichungen), die sich aus der Kurve und der Tabelle ergeben, sind

(1) f(0) = 0 Û i = 0
(2) f (25) = 60 Û a·25⁷ + b·25⁶ + c·25⁵ + d·25⁴ + e·25³ + g·25² + h·25 = 60
(3) f (50) = 90 Û a·50⁷ + b·50⁶ + c·50⁵ + d·50⁴ + e·50³ + g·50² + h·50 = 90
(4) f (75) = 100 Û a·75⁷ + b·75⁶ + c·75⁵ + d·75⁴ + e·75³ + g·75² + h·75 = 100
(5) f '(75) = 0 Û 7·a·75⁶ + 6·b·75⁵ + 5·c·75⁴ + 4·d·75³ + 3·e·75² + 2·g·75 + h = 0
(6) f(100) = 75 Û a·100⁷ + b·100⁶ + c·100⁵ + d·100⁴ + e·100³ + g·100² + h·100 = 75
(7) f(125) = 50 Û a·125⁷ + b·125⁶ + c·125⁵ + d·125⁴ + e·125³ + g·125² + h·125 = 50
(8) f(150) = 25 Û a·150⁷ + b·150⁶ + c·150⁵ + d·150⁴ + e·150³ + g·150² + h·150 = 25  

DERIVE liefert nun als Lösung:
(Dazu benutzt man entweder den Befehl
SOLVE([F(0)=0, F(25)=60, ...],[a,b,c,d,e,g,h,i]) oder man löst das oben angegebene Gleichungssystem mit dem Befehl SOLVE > SYSTEM.)

   

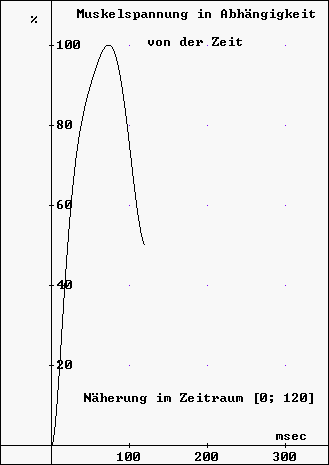
Da die gefundene Funktion nur eine Näherung im Bereich [0 msec; 120 msec] darstellt, kann man nun mittels der CHI-Funktion den zugehörigen Graphen im Bereich [0; 120] im Graphikfenster von DERIVE veranschaulichen. Mittels der Befehlszeile CHI(0,x,120)*F(x) , die dann nur noch berechnet werden muss (vgl. DERIVE-File Muskel.mth ), erhält man dann folgende (Teil-)Kurve: